Virus capsids are pretty
Brief: The majority of virus protein coats (capsids) are in the shape of an icosahedron — a figure with twenty equilateral triangles. The first time I saw this rendered was in a paper by David S. Goodsell. In it, Goodsell describes proteins with structural symmetries. Four viruses are used as examples — they are tobacco necrosis virus (2BUK), tomato bushy stunt virus (2TBV), bluetongue virus (3IYK) and simian virus 40 (1SVA) linked here to their RSCB PDB entries.
Pretty, aren’t they? Very pretty.
If you follow the PDB links, you can take a look at how a single tessellation unit appears, how long a chain is and how massive the capsid is.
Notice: The icosahedron (twenty equilateral triangles) must not be confused with the dodecahedron (twenty points).
C# & Bioinformatics: Indexers & Substitution Matrices
I’ve recently come to appreciate the convenience of C# indexers. What indexers allow you to do is to subscript an object using the familiar bracket notation. I’ve used them for substitution matrices as part of my phylogeny project. Indexers are essentially syntactical sugar that obey the rules of method overloading. I first describe what I think are useful substitution matrix indexers and then a bare bones substitution matrix class (you could use your own). The indexer notation implementation is discussed last, so feel free to skip the preamble if you’re able to deduce what I’m doing.
Note: I’ve only discussed accessors (getters) and not mutators (setters) today.
Some Reasonable Substitution Matrix Indexers
This is the notation you might expect from the indexer notation in C#.
// Let there be a class called SubMatrix which contains data from BLOSUM62.
var sm = new SubMatrix( ... );
// I'll assume you already have some constructors.
int index_of_proline = sm['P'];
// Returns the row or column that corresponds to proline, 14.
char token_at_three = sm[3];
// Returns the amino acid at position three, aspartate.
int score_proline_to_aspartate = sm['P', 'D'];
// Returns the score for a mutation from proline to aspartate, -1.
int score_aspartate_to_proline = sm[3, 14];
// Returns the score for a mutation from aspartate to proline, -1.
An Example Bare Bones Substitution Matrix Class
Let’s say you’ve loaded up the BLOSUM62 and are representing it internally in some 2D array…
// We've keying the rows and columns in the order given by BLOSUM62: // ARNDCQEGHILKMFPSTWYVBZX* (24 rows, columns) int[,] imatrix;
For convenience, let’s say you’ll also keep a dictionary to map at which array position one finds each amino acid…
// Keys = amino acid letters, Values = row or column index Dictionary<char, int> indexOfAA;
Finally, we’ll put these two elements into a class and assume that you’ve already written your own constructors that will take care of the above two items — either from accepting arrays and strings as arguments or by reading from raw files. If this isn’t true and you need more help, feel free to leave a comment and I’ll extend this bare bones example.
// Bare bones class ...
public partial class SubMatrix {
// Properties ...
private int[,] imatrix;
private Dictionary<char, int> indexOfAA;
// Automatic Properties ...
public int Width { // Returns number of rows of the matrix.
get {
return imatrix.GetLength(0);
}
}
// Constructors ...
...
}
I’ve added the automatic property “Width” above — automatic properties are C# members that provide encapsulation: a public face to some arbitrary backend data — you’ve been using these all along when you’ve called “List.Count” or “Array.Length“.
Substitution Matrix Indexer Implementation
You can implement the example substitution matrix indexers as follows. Notice the use of the “this” keyword and square[] brackets[] to specify[] arguments[].
//And finally ...
public partial class SubMatrix {
// Indexers ...
// Give me the row or column index where I can find the token "aa".
public int this[char aa] {
get {
return this.indexOfAA[aa];
}
}
// Give me the amino acid at the row or column index "index".
public char this[int index] {
get {
return this.key[index];
}
}
// Give me the score for mutating token "row" to token "column".
public double this[char row, char column] {
get {
return this.imatrix[this.indexOfAA[row], this.indexOfAA[column]];
}
}
// Give me the score for mutating token at index "row" to index "column".
public double this[int row, int column] {
get {
return this.imatrix[row, column];
}
}
}
Similar constructs are available in Python and Ruby but not Java. I’ll likely cover those later as well as how to set values too.
C# & Bioinformatics: Align Strings to Edit Strings
This post follows roughly from the e-strings (R. Edgar, 2004) topic that I posted about here. The previous source code was listed in Ruby and JS, but this time I’ve used C#.
In this post, I discuss alignment strings (a-strings), then why and how to convert them into edit strings (e-strings). Incidentally, I can’t seem to recover where I first saw alignment strings so tell me if you know.
Alignment strings
When you perform a pairwise sequence alignment, the transformation that you perform on the two sequences is finite. You can record precisely where insertions, deletions and substitutions (or matches) are made. This is useful if you want to retain the original sequences, or later on build a multiple sequence alignment while keeping the history of modifications. There’s a datastructure I’ve seen described called alignment strings, and in it you basically list out the characters ‘I’, ‘D’ and ‘M’ to describe the pairwise alignment.
Consider the example two protein subsequences below.
gi|115372949: GQAGDIRRLQSFNFQTYFVRHYN gi|29827656: SLSTGVSRSFQSVNYPTRYWQ
A global alignment of the two using the BLOSUM62 substitution matrix with the gap penalties -12 to open, -1 to extend yields the following.
gi|115372949: GQAGDIR-----RLQSFNFQTYFVRHYN gi|29827656: SL----STGVSRSFQSVNYPT---RYWQ
The corresponding alignment string looks like this…
gi|115372949: GQAGDIR-----RLQSFNFQTYFVRHYN gi|29827656: SL----STGVSRSFQSVNYPT---RYWQ Align String: MMDDDDMIIIIIMMMMMMMMMDDDMMMM
Remember, the alignment is described such that the top string is modelled as occurring earlier than the bottom string which occurs later — this is why a gap in the top string is an insertion (that new material is inserted in the later, bottom string) while a gap in the bottom string is a deletion (that material is deleted to make the later string). Notice in reality, it doesn’t really matter what’s on top and what’s on bottom– the important thing is that the alignment now contains gaps.
Why we should probably use e-strings instead
An alignment string describes the relationship between two strings and their gaps — we are actually recording some redundant information if we only want to take one string at a time into consideration and the path needed to construct profiles it participates in. The top and bottom sequences are also treated differently, where both ‘M’ and ‘D’ indicates retention of the original characters for the top string and both ‘M’ and ‘I’ indicates retention for the bottom string; the remaining character of course implies the inclusion of a gap character. A pair of e-strings would give each of these sequences their own data structure and allow us to cleanly render the sequences as they appear in the deeper nodes of a phylogenetic tree using the multiply operation described last time.
Here are the corresponding e-strings for the above examples.
gi|115372949: GQAGDIR-----RLQSFNFQTYFVRHYN e-string: < 7, -5, 16 > gi|29827656: SL----STGVSRSFQSVNYPT---RYWQ e-string: < 2, -4, 16, -3, 4 >
Recall that an e-string is a list of alternating positive and negative integers; positive integers mean to retain a substring of the given length from the originating sequence, and negative integers mean to place in a gap of the given length.
Converting a-strings to e-strings
Below is a C# code listing for an implementation I used in my project to convert from a-strings to the more versatile e-strings. The thing is — I really don’t use a-strings to begin with anymore. In earlier versions of my project, I used to keep track of my movement across the score matrix using an a-string by dumping down a ‘D’ for a vertical hop, a ‘I’ for a horizontal hop and a ‘M’ for a diagonal hop. I now just count the number of relevant steps to generate the matching pair of e-strings.
The function below, astring_to_estring takes an a-string (string u) as an argument and returns two e-strings in a list (List<List<int>>) — don’t let that type confuse you, it simply breaks down to a list with two elements in it: the e-string for the top sequence (List<int> v), and the e-string for the bottom sequence (List<int> w).
public static List<List<int>> astring_to_estring(string u) {
/* Defined elsewhere are the constant characters ...
EDITSUB = 'M';
EDITINS = 'I';
EDITDEL = 'D';
*/
var v = new List<int>(); // Top e-string
var w = new List<int>(); // Bottom e-string
foreach(var uu in u) {
if(uu == EDITSUB) { // If we receive a 'M' ...
if(v.Count == 0) { // Working with e-string v (top, keep)
v.Add(1);
} else if(v[v.Count -1] <= 0) {
v.Add(1);
} else {
v[v.Count -1] += 1;
}
if(w.Count == 0) { // Working with e-string w (bottom, gap)
w.Add(1);
} else if(w[w.Count -1] <= 0) {
w.Add(1);
} else {
w[w.Count -1] += 1;
}
} else if(uu == EDITINS) { // If we receive a 'I' ...
if(v.Count == 0) { // Working with e-string v (top, gap)
v.Add(-1);
} else if(v[v.Count -1] >= 0) {
v.Add(-1);
} else {
v[v.Count -1] -= 1;
}
if(w.Count == 0) { // Working with e-string w (bottom, keep)
w.Add(1);
} else if(w[w.Count -1] <= 0) {
w.Add(1);
} else {
w[w.Count -1] += 1;
}
} else if(uu == EDITDEL) { // If we receive a 'D' ...
if(v.Count == 0) { // Working with e-string v (top, keep)
v.Add(1);
} else if(v[v.Count -1] >= 0) {
v[v.Count -1] += 1;
} else {
v.Add(1);
}
if(w.Count == 0) { // Working with e-string w (bottom, keep)
w.Add(-1);
} else if(w[w.Count -1] >= 0) {
w.Add(-1);
} else {
w[w.Count -1] -= 1;
}
}
}
var vw = new List<List<int>>(); // Set up return list ...
vw.Add(v); // Top e-string v added ...
vw.Add(w); // Bottom e-string w added ...
return vw;
}
The conversion back from e-strings to a-strings is also easy, but I don’t cover that today. Enjoy and happy coding 😀
Bioinformatics: Edit Strings (Ruby, JavaScript)
>>> Attached: ( editStringAdder.rb — in Ruby | editStrings.js — in JavaScript ) <<<
I wanted to share something neat that I’ve been using in the phylogeny analyzing software I’ve been developing. In the MUSCLE3 BMC Bioinformatics paper (Robert Edgar, 2004), Edgar describes a way to describe all the changes required to get from one raw sequence to how it appears somewhere in an internal node, riddled with gaps. He calls the data structures Edit Strings (e-strings).
I started using these things in my visualizer because it is a convenient way to describe how to render a profile of sequences at internal nodes of my phylogenetic trees. Rather than storing a copy of the sequence with gaps at each of its ancestors, e-strings allow you to store a discrete pathway of the changes your alignment algorithm made to a sequence at each node.
You can chain e-strings together with a multiply operation so that the profile of any node in the tree can be created out of just the original primary sequences of the dataset (the taxa) and the set of corresponding e-strings for the given tree. You can choose to store the alphabet-distribution profiles this way at each node too, but I decided to use the e-strings only for my visualizer (where seeing each sequence within a profile is important).
Edit strings take the form of a sequence of alternating positive and negative integers; positive integers mean “retain a substring of this length” while negative integers mean “insert gaps of this length” — here’s a few example applications of edit strings on the sequence “ABCDEFGHI“:
<10>("ABCDEFGHIJ") = "ABCDEFGHIJ"
<10 -3>("ABCDEFGHIJ") = "ABCDEFGHIJ---"
<4, -2, 6>("ABCDEFGHIJ") = "ABCD--EFGHIJ"
<2, -1, 5, -4, 3>("ABCDEFGHIJ") = "AB-CDEFG----HIJ"
A few particulars should be mentioned. An application of an e-string onto a sequence is only defined when the sum of the positive integers equals the length of the sequence. The total number of negative integers is arbitrary, and refers to any number of inserted gaps. Finally, a digit zero is meaningless. Edit strings can be multiplied together. If you apply two edit strings in succession onto a sequence, the result is the same as if you had applied the product of two edit strings onto that same sequence. Here are some examples of edit strings multipled together.
<10> * <10> = <10> <10> * <7, -1, 2> = <7, -1, 2> <6, -1, 4> * <7, -1, 3, -2, 1> = <6, -2, 3, -2, 1> <6, -1, 4> * <3, -1, 3, -1, 3, -1, 2> = <3, -1, 3, -2, 2, -1, 2> <6, -1, 4> * <2, -1, 6, -5, 3> = <2, -1, 4, -1, 1, -5, 3>
The multiply function is a bit tricky to implement at first, but one can work backward from the result to get the intermediate step that’s performed mentally. The last two examples above can manually calculated if we imagine an intermediate step as follows. We convert the first e-string to its application on a sequence of ‘+’ symbols– in both the below cases, this results in ten ‘+’ symbols with one ‘-‘ (gap) inserted after the sixth position. We then apply the second edit string to the result of the first application. Finally, we write out the total changes as an e-string on the original sequence of ten ‘+’ symbols. Don’t worry, we don’t really do this in real life software — it’s just a good way for human brains to comprehend the overall operation.
Second last example above — expanded out…
<6, -1, 4> * <3, -1, 3, -1, 3, -1, 2> = ... ++++++-++++ * <3, -1, 3, -1, 3, -1, 2> = ... +++-+++--++-++ = <3, -1, 3, -2, 2, -1, 2>
Last example above — expanded out…
<6, -1, 4> * <2, -1, 6, -5, 3> = ... ++++++-++++ * <2, -1, 6, -5, 3> = ... ++-++++-+-----+++ = <2, -1, 4, -1, 1, -5, 3>
Here’s the code in Ruby for my take on the multiply function. I derived my version of the function based on the examples from Edgar’s BMC paper (mentioned before). When you think about it, the runtime is the sum of the number of elements of the two e-strings being multiplied. This becomes obvious when you realize that the only computation that really occurs is when a positive integer is encountered in the second e-string. The function is called estring_product(), it takes two e-strings as arguments (u, v) and returns a single e-string (w). This function internally calls an estring_collapse() function because we intermediately create an e-string that may have several positive integers or several negative integers in a row (when this happens, it’s usually just two in a row). Consecutive same-signed integers of an e-string are added together.
def estring_product(u, v)
w = []
uu_replacement = nil
ui = 0
vi = 0
v.each do |vv|
if vv < 0
w << vv
elsif vv > 0
vv_left = vv
uu = uu_replacement != nil ? uu_replacement : u[ui]
uu_replacement = nil
until vv_left == 0
if vv_left >= uu.abs
w << uu
vv_left -= uu.abs
ui += 1
uu = u[ui]
else
if uu > 0
w << vv_left
uu -= vv_left
elsif uu < 0
w << -vv_left
uu += vv_left
end
vv_left = 0
uu_replacement = uu
end
end
end
vi += 1
end
return estring_collapse(w)
end
If you aren’t familiar with Ruby, the “<<” operator means “append the right value to the left collection”. Everything else should be pretty self-explanatory (leave a comment if it’s not).
def estring_collapse(u)
v = []
u.each do |uu|
if v[-1] == nil
v << uu
elsif (v[-1] <=> 0) == (uu <=> 0)
v[-1] += uu
else
v << uu
end
end
return v
end
The “<=>” lovingly referred to as the spaceship operator compares the right value to the left value; if the right value is greater, then the result is 1.0; if the left value is greater, then the result is -1.0; if the left and right values are the same, then the result is 0.0.
A Few Notes on the Attached Files (Ruby, Javascript)
The Ruby source has a lot of comments in it that should help you understand when and where to use the included two functions. The Javascript is actually used in a visualizer I’ve deployed now so it has a few more practical functions in it. A function called sequence_estring() is included that takes a $sequence and applies an $estring, then returns a new gapped sequence. A utility signum() function is included which takes the place of the spaceship operator in the Ruby version. A diagnostic function, p_uvw() is included that just uses document.write() to print out whatever you give as (estring) $u, (estring) $v and (estring) $w. Finally, the JavaScript functions sequence_estring() and estring_product() will print out error messages with document.write() when the total sequence length specified in the first argument is not the same as the total sequence length implied by the second argument. Remember, the sum of the absolute values of the first argument describes the total length of the sequence– each of these tokens must be accounted for by the positive values of the second argument, the estring that will operate on it.
The Null Coalescing Operator (C#, Ruby, JS, Python)
Null coalescence allows you to specify what a statement should evaluate to instead of evaluating to null. It is useful because it allows you to specify that an expression should be substituted with some semantic default instead of defaulting on some semantic null (such as null, None or nil). Here is the syntax and behaviour in four languages I use often — C#, Ruby, JavaScript and Python.
C#
Null coalescencing in C# is very straight forward since it will only ever accept first class objects of the same type (or null) as its operator’s arguments. This restriction is one that exists at compile time; it will refuse to compile if it is asked to compare primitives, or objects of differing types (unless they’re properly cast).
Syntax:
<expression> ?? <expression>
(The usual rules apply regarding nesting expressions, the use of semi-colons in complete statements etc..)
A few examples:
DummyNode a = null; DummyNode b = new DummyNode(); DummyNode c = new DummyNode(); return a ?? b; // returns b return b ?? a; // still returns b DummyNode z = a ?? b; // z gets b return a ?? new DummyNode(); // returns a new dummy node return null ?? a ?? null; // this code has no choice but to return null return a ?? b ?? c; // returns b -- the first item in the chain that wasn't null
No, you’d never really have a bunch of return statements in a row like that — they’re only there to demonstrate what you should expect.
Ruby, Python and Javascript
These languages are less straight forward (i.e. possess picky nuances) since they are happy to evaluate any objects of any class with their coalescing operators (including emulated primitives). These languages however disagree about what the notion of null should be when it comes to numbers, strings, booleans and empty collections; adding to the importance of testing your code!
Syntax for Ruby, Javascript:
<expression> || <expression>
Syntax for Ruby, Python:
<expression> or <expression>
(Ruby is operator greedy :P.)
The use of null coalescence in these languages are the same as they are in C# in that you may nest coalescing expressions as function arguments, use them in return statements, you may chain them together, put in an object constructor as a right-operand expression etc.; the difference is in what Ruby, Python or Javascript will coalesce given a left-expression operand. The below table summarizes what left-expression operand will cause the statement to coalesce into the right-expression operand (i.e. what the language considers to be ‘null’-ish in this use).
| Expression as a left-operand | Does this coalesce in Ruby? | Does this coalesce in Python? | Does this coalesce in JavaScript? |
| nil / None / null | Yes | Yes | Yes |
| [] | No | Yes | No |
| {} | No | Yes | n/a* |
| 0 | No | Yes | Yes |
| 0.0 | No | Yes | Yes |
| “” | No | Yes | Yes |
| ” | No | Yes | Yes |
| false / False / false |
Yes | Yes | Yes |
*Note that in JavaScript, you’d probably want to use an Object instance as an associative array (hash) so that the field names are the keys and the field values are the associated values — doing so means that you can never have a null associative array.
Contrast the above table to what C# will coalesce: strictly “null” objects only.
The null coalescing operator makes me happy. Hopefully it’ll make you happy too.
Parsing a Newick Tree with recursive descent
>>> Attached: ( parse_newick.js – implementation in JS | index.html – example use ) <<<
Update: Fixed parse_newick.js source code that caused a field to be mislabelled in index.html (2010 Dec. 19)
This method of parsing works for any language that allows recursive functions — basically any of the curly bracket languages (C#, C, Java) and the fast-development languages (Ruby, JavaScript, Python) can do this. This particular example will include JavaScript code which you can take and do whatever you want with — recursive descent parsing is a well-known and solved problem, so it’s no skin off my back. Before we begin, I should probably explain what a tree in Newick format is.
What exactly is the Newick format?
Remember back in second year CS when your data structures / abstract data types / algorithms instructor said you can represent any tree as a traversal? Well, if not — don’t fret, it’s not hard to get the hang of.
A traversal is a finite, deterministic representation of a tree which can be thought of as a road map of how to visit each node of the tree exactly once. The phylogeny / bioinformatics people will know each of these nodes as either taxa / sequences (the leaves) or profiles (the internal nodes — i.e. not the leaves). A tree in Newick format is exactly that — a traversal. More specifically, it is a depth-first post-order traversal. When traversing a tree, we have a few options about how we want to visit the nodes — depth-first post-order means we want to start at the left-most, deepest leaf, and recursively visit all of the nodes before we end at the root.
A tree expressed in Newick format describes a tree as an observer has seen it having visited each node in a depth-first post-order traversal.
A node in the Newick format can be…
- A leaf in the form: “<name>:<branch_length>”
- e.g. “lcl|86165:-0“
- e.g. “gi|15072471:0.00759886“
- e.g. “gi|221105210:0.00759886“
- Or a node in the form “(<node>,<node>):<branch_length>”
- This is where it gets tricky and recursive — the “node” item above can be another node, or a leaf — when a node is composed of at least another node, we call that a recursive case; when a node is composed of only leaves, we call that a base case. We make this clearer in the next section.
- Or a node in the form “(<node>,<node>);”
- The semi-colon at the end means that we have finished describing the tree. There is no branch length as the root of the tree is not connected to a parent.
Understanding recursion in a Newick Tree
Base case e.g.: The below node is composed of two leaves.
“(lcl|86165:-0,gi|87118305:-0):0.321158”
Recursive case e.g.: The below node is composed of a leaf on the left, and another node on the right; this right-node is composed of two leaves.
“(gi|71388322:0.0345038,(gi|221107809:0.00952396,gi|221101741:0.00952396):0.0249798):0.0111081“
If the names look a bit funny, that’s because these are sequences pulled out of a blastp search.
The Newick tree itself may have any number of nodes, the base case being a single node. The only restriction is that any node either is a leaf (has zero children) or must have two children (never a single child). These two children again are allowed to be either leaves or other nodes.
We would visualize the above Recursive case e.g. as follows.:
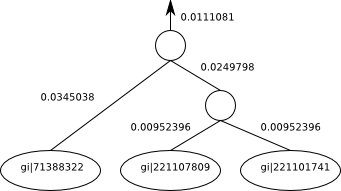
Where the numbers beside the edges are edge length and the names of the named taxa are indicated inside the circles (leaves). The unnamed internal nodes are the profiles that have been calculated with alignments. You’ll notice that there’s a branch length leading out of the root of this subtree into the rest of the tree (not shown). If this was a complete tree on its own, the root would have no branch length there and no arrow coming out of it.
Finally, Parsing!
Now that we have reviewed the depth-first post-order traversal, the Newick format and how to interpret it; we can move onto parsing these things. In parsing, we hope to create an in-memory structure that represents the tree. The parser I discuss assumes that the Newick format string already has had all newlines stripped, as it uses regular expressions. If your trees aren’t stored that way, just make sure that newlines are stripped before feeding it into my function. The in-memory object that’s created will have the following fields as a minimum.
- node_type $left – the left child of a node
- node_type $right – the right child of a node
- string_type $name – the name of a node (if it is a leaf)
- float_type $branch_length – the length of the branch coming out of the top of a given node
I also use the following two fields to keep track of a few house keeping items and to make life pleasant for future tasks with this in-memory structure.
- node_type $parent – the parent of a node
- integer_type $serial – the order in which this node occurs when parsed
Note that in future, a depth-first post-order traversal will yield the nodes in the exact order that they were read — so in reality “this.serial” isn’t really needed, but it’s nice to have for future functions you might write as a shorthand. Have you understood why these nodes would occur in the same order?
Each language has its own quirks. Python and JavaScript have the advantage that you can define a class and define its properties (fields) on the fly — meaning there’s less code to download and to write, which is particularly good for blogs 😛
Here’s pseudo-code for the recursive descent parsing function “tree_builder(<newick_string>)” — I don’t indicate where to strip away newlines because I assume they’re gone. I also don’t indicate where to strip away whitespace (I did previously, but that took up like half the pseudocode). So if there’s a place where you suspect whitespace can occur, strip it away and increment the cursor by the length of that whitespace.
Note: We are assuming that there are no newlines in the file — that is, the entire newick traversal is one string on a single long unbroken line.
// Note:
// Call tree_builder() with a "new" operator in JavaScript
// to allow it to use the 'this' keyword.
// In other languages,
// you may need to explicitly create a new object instead of using 'this'.
var count = 0; // can be either a global variable or a reference
// keeps track of how many nodes we've seen
var cursor = 0; // also either a global or a reference
// keeps track of where in the string we are
function tree_builder(newick_string) {
// Look for things relating to the left child of this node //
if $newick_string [ $cursor ] == "(" {
$cursor ++; // move cursor to position after "(".
if newick_string [ $cursor ] == "(" {
// Then the $left node is an internal node: requires recursion //
$this.left = new tree_builder(newick_string); // RECURSIVE CALL.
$this.left.parent = $this;
}
// try to find a valid $name next at the current cursor position //
if $name = $newick_string [ $cursor ] . regex match ("^[0-9A-Za-z_|]+") {
// Then the $left node is a leaf node: parse the leaf data //
$this.left = new Object;
$this.left.name = $name;
$this.left.serial = $count;
$count ++;
$this.left.parent = $this;
$cursor += length of $name;
// move cursor to position after matched name.
}
// notice: if no $name found, just skip to finding branch length.
}
if $newick_string [ $cursor ] == ":" {
// Expect left branch length after descending into the left child //
$cursor ++; // move cursor to position after the colon.
// look for the string representation of a floating point value "FPV"...
$branch_length_string =
$newick_string [ $cursor ] . regex match ("^[0-9.+eE-]+");
$this.$left.$score = $branch_length_string as a FPV;
$cursor += length of the string $branch_length_string;
// move cursor after FPV.
}
// Look for things related to the right node //
if $newick_string [ $cursor ] == "," {
$cursor ++; // move cursor after the comma
if newick_string [ $cursor ] == "(" {
// Then the $right node is an internal node: requires recursion //
$this.right = new tree_builder($newick_string); // RECURSIVE CALL.
$this.right.parent = $this;
}
// try to find a valid $name next at the current cursor position //
if $name = $newick_string [ $cursor ] . regex match ("^[0-9A-Za-z_|]+") {
// Then the $right node is a leaf node: parse the leaf data //
$this.right = new Object;
$this.right.name = $name;
$this.right.serial = $count;
$serial ++;
$this.right.parent = $this;
$cursor += $length of $name;
}
// again, accept if no $name found and move onto branch length.
}
// Now looking for the branch length ... //
if $newick_string at $cursor == ":" {
// Expect right branch length after descending into right child //
$cursor ++; // moving past the colon.
$branch_length_string =
$newick_string [ $cursor ] . regex match ("^[0-9.+eE-]+");
$this.right.score = $branch_length_string as a FPV;
$cursor += length of the string $branch_length_string;
}
if $newick_string at $cursor == ")" {
$cursor ++; // move past ")".
}
// Expect the branch length of $this node after analyzing both children //
if $newick_string at $cursor == ":" {
$cursor ++;
$branch_length_string =
$newick_string [ $cursor ] . regex match ("^[0-9.+eE-]+");
$this.score = $branch_length_string as a FPV;
$cursor += length of the string $branch_length_string;
}
if $newick_string at $cursor == ";" {
// This case only executes for the root node-- //
// --the very last node to finish parsing //
$cursor ++; // to account for the semicolon (optional, consistency)
$this.serial = $count; // no need to increment $count here
}
// Return to complete a recursive instance (internal) or base case (leaf) //
return this; // not needed if "new" operator was used all along
}
The implementation that’s included in the attached JavaScript does two things differently than the above. First, I don’t force the user to break encapsulation by declaring globals. Instead, I use an object called “ref” which has two fields, “ref.count” and “ref.cursor”. The name “ref” is chosen to remind us that its fields are passed by reference. This is possible because the object “ref” itself is passed by reference (I could have called it anything, but I chose a name that suited its purpose). Imagine trying to pass “count” and “cursor” in this recursive function without an enclosing object — what would happen instead is that the value wouldn’t be updated, instead the integer values would be copied and modified locally in the span of single function instances. The “ref” object is passed as an argument to the “_tree_builder(<ref>, <newick_string>)” function internally where it is instantiated if “null” is passed in the place of “ref”. The calling user doesn’t even need to know about it, as it’s all wrapped together in a pretty package and the user just calls “tree_builder(<newick_string>)” as before — without the need for globals. The enclosing function even does the work of instantiating the root node with the “new” keyword so that the end user doesn’t even need to (and shouldn’t!) say “new”.
Finally, there is a traversal function, and an expose function. The traversal function returns the node objects in an array following in the natural depth-first post-order described previously. The expose function is a debugging function which writes the output using “thoughts_write(<message>)” which wraps “document.write(<message>)”. You can change “thoughts_write(<message>)” to print output elsewhere using “document.getElementById(<some_identity>).innerHTML += (<message>)” where “some_identity” is the “id” of some element in your HTML. Without going into detail, the traversal function also uses an internal “ref” object which refers to the array as it is filled.
Some other things you can try…
The JavaScript recursive descent parser is actually a simplified version of something that I threw together earlier. The major difference is that I tag leaf nodes with fasta protein sequences by passing a reference to an associative array (or hash) as an argument to “tree_builder(<newick_string>, <fasta_hash>)”. Remember, in JavaScript, an associative array is an instance of an Object, not an instance of an Array. Using non-integer field names in an Array is actually not well defined but kind of sort of works semi-consistently between browsers (i.e. don’t try!), but that’s a story for another day. Whenever the name of a leaf is parsed, I would look it up in the hash and put it in a field either “this.left.fasta” or “this.right.fasta” thereby conferring to the leaf nodes of the in-memory structure the appropriate fasta protein sequence.
Lessons Learned
In putting this thing together, I managed to relearn JS, recursive descent parsing and making JS pass things by reference up and down a recursive stack of function calls. Andre Masella helpfully reminded me that I didn’t need to use any kind of BNF or LALR(1) parser — just an easy single-function parser would do. This is actually a port of a C# parser which does the same thing that I wrote in an earlier step for phylogenetic analysis — the difference being that C# offers a “ref” keyword that allows one to specify arguments in a function’s parameter list as emulated references (functionally equivalent to using C’s asterisk and ampersand convention though not operationally equivalent).
Happy parsing! The code presented should be easy enough to understand for you to port it into the language of your choice for whatever purposes you design.
 Ed's Big Plans
Ed's Big Plans