Archive for March, 2011
SOM Indexing Logic
Update: Added some code too.
Brief: A classmate and I started talking about how we implemented the Kohonen Self Organizing Maps (SOM)s. I used C and indexed first the rows and the columns of the SOM before the index corresponding to the weight vectors (same as the index for the input vectors); he used C++ and indexed the weight vectors first before the columns and the rows.
Either way, we could use a three-deep array like this (switching the indexers as appropriate) …
const double low = 0.0; // minimum allowed random value to initialize weights
const double high = 1.0; // maximum allowed random value to initialize weights
const int nrows = 4; // number of rows in the map
const int ncolumns = 4; // number of columns in the map
const int ninputs = 3; // number of elements in an input vector, each weight vector
double*** weight; // the weight array
weight = calloc(nrows, sizeof(double**));
for(int r = 0; r < nrows; r ++) {
weight[r] = calloc(ncolumns, sizeof(double*));
for(int c = 0; c < ncolumns; c ++) {
weight[r] = calloc(ninputs, sizeof(double));
for(int i = 0; i < ninputs; i ++) {
weight[r][i] =
(((double)random() / (double)INT_MAX) * (high - low)) + low;
}
}
}
In the below diagram, the left side is a schematic of his approach and the right side is a schematic of my approach.
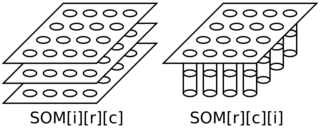
Figure above: SOM Indexing — Left (his): SOM indexed as input, row, column; Right (mine): SOM indexed as row, column, input.
Both schematics in the above diagram have four rows and four columns in the map where each weight (and input) vector has three elements.
I think my logic is better since we’ll often be using some distance function to evaluate how similar a weight vector is to a given input — to me, it’s natural to thus index these at the inner most nesting while looping over the rows and columns of the map.
The opposing approach was apparently used because my classmate had previously developed a matrix manipulation library. I’m actually kind of curious to take a look at it later.
SOM in Regression Data (animation)
The below animation is what happens when you train a Kohonen Self-Organizing Map (SOM) using data meant for regression instead of clustering or classification. A total of 417300 training cycles are performed — a single training cycle is the presentation of one exemplar to the SOM. The SOM has dimensions 65×65. Exemplars are chosen at random and 242 snapshots are taken in total (once every 1738 training cycles).
 Ed's Big Plans
Ed's Big Plans