Archive for June, 2010
Parsing a Newick Tree with recursive descent
>>> Attached: ( parse_newick.js – implementation in JS | index.html – example use ) <<<
Update: Fixed parse_newick.js source code that caused a field to be mislabelled in index.html (2010 Dec. 19)
This method of parsing works for any language that allows recursive functions — basically any of the curly bracket languages (C#, C, Java) and the fast-development languages (Ruby, JavaScript, Python) can do this. This particular example will include JavaScript code which you can take and do whatever you want with — recursive descent parsing is a well-known and solved problem, so it’s no skin off my back. Before we begin, I should probably explain what a tree in Newick format is.
What exactly is the Newick format?
Remember back in second year CS when your data structures / abstract data types / algorithms instructor said you can represent any tree as a traversal? Well, if not — don’t fret, it’s not hard to get the hang of.
A traversal is a finite, deterministic representation of a tree which can be thought of as a road map of how to visit each node of the tree exactly once. The phylogeny / bioinformatics people will know each of these nodes as either taxa / sequences (the leaves) or profiles (the internal nodes — i.e. not the leaves). A tree in Newick format is exactly that — a traversal. More specifically, it is a depth-first post-order traversal. When traversing a tree, we have a few options about how we want to visit the nodes — depth-first post-order means we want to start at the left-most, deepest leaf, and recursively visit all of the nodes before we end at the root.
A tree expressed in Newick format describes a tree as an observer has seen it having visited each node in a depth-first post-order traversal.
A node in the Newick format can be…
- A leaf in the form: “<name>:<branch_length>”
- e.g. “lcl|86165:-0“
- e.g. “gi|15072471:0.00759886“
- e.g. “gi|221105210:0.00759886“
- Or a node in the form “(<node>,<node>):<branch_length>”
- This is where it gets tricky and recursive — the “node” item above can be another node, or a leaf — when a node is composed of at least another node, we call that a recursive case; when a node is composed of only leaves, we call that a base case. We make this clearer in the next section.
- Or a node in the form “(<node>,<node>);”
- The semi-colon at the end means that we have finished describing the tree. There is no branch length as the root of the tree is not connected to a parent.
Understanding recursion in a Newick Tree
Base case e.g.: The below node is composed of two leaves.
“(lcl|86165:-0,gi|87118305:-0):0.321158”
Recursive case e.g.: The below node is composed of a leaf on the left, and another node on the right; this right-node is composed of two leaves.
“(gi|71388322:0.0345038,(gi|221107809:0.00952396,gi|221101741:0.00952396):0.0249798):0.0111081“
If the names look a bit funny, that’s because these are sequences pulled out of a blastp search.
The Newick tree itself may have any number of nodes, the base case being a single node. The only restriction is that any node either is a leaf (has zero children) or must have two children (never a single child). These two children again are allowed to be either leaves or other nodes.
We would visualize the above Recursive case e.g. as follows.:
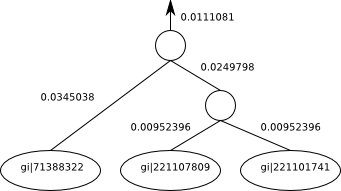
Where the numbers beside the edges are edge length and the names of the named taxa are indicated inside the circles (leaves). The unnamed internal nodes are the profiles that have been calculated with alignments. You’ll notice that there’s a branch length leading out of the root of this subtree into the rest of the tree (not shown). If this was a complete tree on its own, the root would have no branch length there and no arrow coming out of it.
Finally, Parsing!
Now that we have reviewed the depth-first post-order traversal, the Newick format and how to interpret it; we can move onto parsing these things. In parsing, we hope to create an in-memory structure that represents the tree. The parser I discuss assumes that the Newick format string already has had all newlines stripped, as it uses regular expressions. If your trees aren’t stored that way, just make sure that newlines are stripped before feeding it into my function. The in-memory object that’s created will have the following fields as a minimum.
- node_type $left – the left child of a node
- node_type $right – the right child of a node
- string_type $name – the name of a node (if it is a leaf)
- float_type $branch_length – the length of the branch coming out of the top of a given node
I also use the following two fields to keep track of a few house keeping items and to make life pleasant for future tasks with this in-memory structure.
- node_type $parent – the parent of a node
- integer_type $serial – the order in which this node occurs when parsed
Note that in future, a depth-first post-order traversal will yield the nodes in the exact order that they were read — so in reality “this.serial” isn’t really needed, but it’s nice to have for future functions you might write as a shorthand. Have you understood why these nodes would occur in the same order?
Each language has its own quirks. Python and JavaScript have the advantage that you can define a class and define its properties (fields) on the fly — meaning there’s less code to download and to write, which is particularly good for blogs 😛
Here’s pseudo-code for the recursive descent parsing function “tree_builder(<newick_string>)” — I don’t indicate where to strip away newlines because I assume they’re gone. I also don’t indicate where to strip away whitespace (I did previously, but that took up like half the pseudocode). So if there’s a place where you suspect whitespace can occur, strip it away and increment the cursor by the length of that whitespace.
Note: We are assuming that there are no newlines in the file — that is, the entire newick traversal is one string on a single long unbroken line.
// Note:
// Call tree_builder() with a "new" operator in JavaScript
// to allow it to use the 'this' keyword.
// In other languages,
// you may need to explicitly create a new object instead of using 'this'.
var count = 0; // can be either a global variable or a reference
// keeps track of how many nodes we've seen
var cursor = 0; // also either a global or a reference
// keeps track of where in the string we are
function tree_builder(newick_string) {
// Look for things relating to the left child of this node //
if $newick_string [ $cursor ] == "(" {
$cursor ++; // move cursor to position after "(".
if newick_string [ $cursor ] == "(" {
// Then the $left node is an internal node: requires recursion //
$this.left = new tree_builder(newick_string); // RECURSIVE CALL.
$this.left.parent = $this;
}
// try to find a valid $name next at the current cursor position //
if $name = $newick_string [ $cursor ] . regex match ("^[0-9A-Za-z_|]+") {
// Then the $left node is a leaf node: parse the leaf data //
$this.left = new Object;
$this.left.name = $name;
$this.left.serial = $count;
$count ++;
$this.left.parent = $this;
$cursor += length of $name;
// move cursor to position after matched name.
}
// notice: if no $name found, just skip to finding branch length.
}
if $newick_string [ $cursor ] == ":" {
// Expect left branch length after descending into the left child //
$cursor ++; // move cursor to position after the colon.
// look for the string representation of a floating point value "FPV"...
$branch_length_string =
$newick_string [ $cursor ] . regex match ("^[0-9.+eE-]+");
$this.$left.$score = $branch_length_string as a FPV;
$cursor += length of the string $branch_length_string;
// move cursor after FPV.
}
// Look for things related to the right node //
if $newick_string [ $cursor ] == "," {
$cursor ++; // move cursor after the comma
if newick_string [ $cursor ] == "(" {
// Then the $right node is an internal node: requires recursion //
$this.right = new tree_builder($newick_string); // RECURSIVE CALL.
$this.right.parent = $this;
}
// try to find a valid $name next at the current cursor position //
if $name = $newick_string [ $cursor ] . regex match ("^[0-9A-Za-z_|]+") {
// Then the $right node is a leaf node: parse the leaf data //
$this.right = new Object;
$this.right.name = $name;
$this.right.serial = $count;
$serial ++;
$this.right.parent = $this;
$cursor += $length of $name;
}
// again, accept if no $name found and move onto branch length.
}
// Now looking for the branch length ... //
if $newick_string at $cursor == ":" {
// Expect right branch length after descending into right child //
$cursor ++; // moving past the colon.
$branch_length_string =
$newick_string [ $cursor ] . regex match ("^[0-9.+eE-]+");
$this.right.score = $branch_length_string as a FPV;
$cursor += length of the string $branch_length_string;
}
if $newick_string at $cursor == ")" {
$cursor ++; // move past ")".
}
// Expect the branch length of $this node after analyzing both children //
if $newick_string at $cursor == ":" {
$cursor ++;
$branch_length_string =
$newick_string [ $cursor ] . regex match ("^[0-9.+eE-]+");
$this.score = $branch_length_string as a FPV;
$cursor += length of the string $branch_length_string;
}
if $newick_string at $cursor == ";" {
// This case only executes for the root node-- //
// --the very last node to finish parsing //
$cursor ++; // to account for the semicolon (optional, consistency)
$this.serial = $count; // no need to increment $count here
}
// Return to complete a recursive instance (internal) or base case (leaf) //
return this; // not needed if "new" operator was used all along
}
The implementation that’s included in the attached JavaScript does two things differently than the above. First, I don’t force the user to break encapsulation by declaring globals. Instead, I use an object called “ref” which has two fields, “ref.count” and “ref.cursor”. The name “ref” is chosen to remind us that its fields are passed by reference. This is possible because the object “ref” itself is passed by reference (I could have called it anything, but I chose a name that suited its purpose). Imagine trying to pass “count” and “cursor” in this recursive function without an enclosing object — what would happen instead is that the value wouldn’t be updated, instead the integer values would be copied and modified locally in the span of single function instances. The “ref” object is passed as an argument to the “_tree_builder(<ref>, <newick_string>)” function internally where it is instantiated if “null” is passed in the place of “ref”. The calling user doesn’t even need to know about it, as it’s all wrapped together in a pretty package and the user just calls “tree_builder(<newick_string>)” as before — without the need for globals. The enclosing function even does the work of instantiating the root node with the “new” keyword so that the end user doesn’t even need to (and shouldn’t!) say “new”.
Finally, there is a traversal function, and an expose function. The traversal function returns the node objects in an array following in the natural depth-first post-order described previously. The expose function is a debugging function which writes the output using “thoughts_write(<message>)” which wraps “document.write(<message>)”. You can change “thoughts_write(<message>)” to print output elsewhere using “document.getElementById(<some_identity>).innerHTML += (<message>)” where “some_identity” is the “id” of some element in your HTML. Without going into detail, the traversal function also uses an internal “ref” object which refers to the array as it is filled.
Some other things you can try…
The JavaScript recursive descent parser is actually a simplified version of something that I threw together earlier. The major difference is that I tag leaf nodes with fasta protein sequences by passing a reference to an associative array (or hash) as an argument to “tree_builder(<newick_string>, <fasta_hash>)”. Remember, in JavaScript, an associative array is an instance of an Object, not an instance of an Array. Using non-integer field names in an Array is actually not well defined but kind of sort of works semi-consistently between browsers (i.e. don’t try!), but that’s a story for another day. Whenever the name of a leaf is parsed, I would look it up in the hash and put it in a field either “this.left.fasta” or “this.right.fasta” thereby conferring to the leaf nodes of the in-memory structure the appropriate fasta protein sequence.
Lessons Learned
In putting this thing together, I managed to relearn JS, recursive descent parsing and making JS pass things by reference up and down a recursive stack of function calls. Andre Masella helpfully reminded me that I didn’t need to use any kind of BNF or LALR(1) parser — just an easy single-function parser would do. This is actually a port of a C# parser which does the same thing that I wrote in an earlier step for phylogenetic analysis — the difference being that C# offers a “ref” keyword that allows one to specify arguments in a function’s parameter list as emulated references (functionally equivalent to using C’s asterisk and ampersand convention though not operationally equivalent).
Happy parsing! The code presented should be easy enough to understand for you to port it into the language of your choice for whatever purposes you design.
URL mangling for HTML forms (a better Mediawiki search box)
Followup: This is better than my previous Mediawiki search box solution because it doesn’t require an extra PHP file (search-redirect.php) to deploy. It relies completely on URL mangling inside the HTML form on the page you are putting the search box. Previous post here.
A valid HTML form input type is “hidden”. What this means is that a variable can be set without a control displayed for it in a form. Other input types for instance are “text” for a line of text and “submit” for the proverbial submit button — both of these input types are displayed. Variables set by the “hidden” input type are treated as normal and are shipped off via the GET or POST method that you’ve chosen for the whole html form…
So, to create the following mangled URL…
https://eddiema.ca/wiki/index.php?title=Special%3ASearch&search=searchterms&go=Go
There are the following variables … with the following values:
- title … “Special%3ASearch” (%3A is the HTML entity “:”)
- search … “searchterms” (the only variable requiring user input)
- go … “Go”
The only variable that needs to be assigned from the form is “search” to which I’ve assigned the placeholder “searchterms” in the above URL.
The form thus needs only to take input for the variable “search” with a “text” type input, while “title” and “go” are already assigned– a job for the “hidden” type input.
Here’s what the simplest form for this would look like…
<form action="https://eddiema.ca/wiki/index.php" method="get"> Search Ed's Wiki Notebook: <input name="title" type="hidden" value="Special:Search" /> <input name="search" type="text" value="" /> <input name="go" type="hidden" value="Go" /> <input type="submit" value="Search" /> </form>
Again, replace the text “Search Ed’s Wiki Notebook” with your own description and replace “https://eddiema.ca/wiki/index.php” with the form handler that you’re using– it’ll either be a bare domain, subdomain or could end with index.php if it’s a Mediawiki installation.
And that’s it! A far simpler solution than last time with the use of the “hidden” type input to assist in URL mangling.
Update: Here’s an even more improved version — this time, the end user doesn’t even see a page creation option when a full title match isn’t found. Demo (hooked up to my wiki) and Code below …
<form id="searchform" action="https://eddiema.ca/wiki/index.php" method="get"> <label class="screen-reader-text" for="s">Search Ed's Wiki Notebook:</label> <input id="s" type="text" name="search" value="" /> <input name="fulltext" type="hidden" value="Search" /> <input id="searchsubmit" type="submit" value="Search" /> </form>
Notice that the variables “Special:Search” and “go” are not actually needed — instead, the variable “fulltext” is assigned the string “Search” — this causes mediawiki to hide the “You can create this page” option.
Add an arbitrary Mediawiki search box anywhere!
Update: A better solution that doesn’t require a separate “search-redirect.php” file has been posted here.
I’ve been looking for this solution for a long time now and I’m happy to have finally found it. Following hints from Dave Taylor and Peter De Decker, I’ve glued together a solution that doesn’t take too much effort and doesn’t require any additional hacking around in SQL.
The objective was to add a search box on the right-column navigation of this blog that would search my wiki notebook. It wasn’t until I stumbled on the above two blogs that I realized I can just mangle URLs to conduct a search on mediawikis! The specific URL used to search my wiki looks a little like this…
https://eddiema.ca/wiki/index.php?title=Special%3ASearch&search=searchterms&go=Go
It might be a bit different for your installation depending on the version that you installed and a few of your settings– to find out what it looks like, search for something and copy down the URL in the address bar.
The file “search-redirect.php” used by Wikipedia takes in your search terms, and mangles those terms into a URL conforming to the above example. It then redirects you to that constructed URL. You can find this used on the main page of Wikipedia as noted by Dave.
My search-redirect.php based on Peter’s work above is two lines long, and looks like this:
<php?
$redirect_url =
"https://eddiema.ca/wiki/index.php?title=Special%3ASearch&search=".
$_GET['search'].
"&go=Go";
@header( "Location: ".$redirect_url );
?>
You probably want to place your own search-redirect.php in the root directory of your wiki installation– however, it looks to me like it doesn’t really matter since the whole URL is rewritten anyway. I bet you can put this file anywhere on the net that supports PHP. The final thing that’s missing is the search box– anything that uses this formula will work:
<form action="https://eddiema.ca/wiki/search-redirect.php" method="get"> Search Ed's Wiki: <input type="text" name="search" /> <input type="submit" value="Search" /> </form>
Putting this code on a page with your own wiki URL as a stem instead of mine will allow you to search your own wiki from any other page.
A Chess Post – S-Chess and Omega Chess
Update: A link for Omega Chess, and a link for Seirawan Chess.
This is the first of a few posts I’d like to make about chess. In particular, this post is about two chess variants. Seirawan Chess (S-Chess) and Omega Chess. These two variants feature the familiar FIDE chess pieces along with two new pieces each. I’ll introduce each variant on their own first.
In Seirawan Chess, one starts with the familiar eight-by-eight board and opening array with the addition of two pieces set aside in reserve. These pieces are the Hawk and the Elephant. The Hawk is a Bishop and Knight compound while the Elephant is a Rook and Knight compound (a compound is a combination of pieces– a Queen is a Rook and Bishop compound). The two pieces that are set aside are placed onto the board when a player moves a piece from the back rank. The piece being dropped onto the board thus occupies the square in the back rank that has just been vacated. One can only place a single reserved piece in a given move. During a castle if the player so chooses, a reserved piece may be dropped on either the King’s or the Rook’s original square; it is not permitted to drop both reserved pieces during a castle.
In Omega Chess, one starts with a ten-by-ten board and an opening array that is flanked by the addition of a Champion and the Champion’s Pawn. The board is also extended diagonally by a single square in each of the four corners– these corner squares are occupied by a Wizard each. In the opening array, each piece is placed behind a Pawn with the exception of the Wizard. The Champion may move one step orthogonally, leap two steps orthogonally or leap two steps diagonally. The Wizard may move one step diagonally or leap (1, 3) — whereas a Knight leaps (1, 2). The Wizard is hence colour bound. The special corner Wizard squares are not actually special– they are just part of the board topology and can be used by all other pieces (except the Rook which cannot leap or slide diagonally into those spots).
For the fun of it, I have been playing Omega Chess with Seirawan Chess dropped pieces and it’s worked quite well so far. The size of the board accommodates well the Seirawan compounds. Additionally, I have been considering a house rule about dropping the Seirawan pieces– perhaps it shouldn’t be allowed that a dropped piece immediately defend the piece that dropped it. For instance, a Bishop dropping a Hawk makes for a very tough defense. A Wizard dropping a Hawk should be allowed however if the Wizard made its oblong (1, 3) leap.
If you see me walking around with a big black tube, I’m probably carrying this chess set. Challenge me to a game 😀
I’ll post some photos and such soon. The design of all the pieces from both sets is remarkably soothing and fits very well into the Staunton style. I was very lucky to discover that the Seirawan pieces are each appropriately tall compared to the Queen of the Omega Chess set I purchased.
One final thing– I decided to score the pieces in this combined game based on the mobility of each of the pieces on the ten-by-ten board. Here are my findings…
| Score | Piece | Remark |
| 29.40 | Queen | FIDE |
| 23.76 | Elephant | Seirawan |
| 18.00 | Rook | FIDE |
| 17.16 | Hawk | Seirawan |
| 11.40 | Bishop | FIDE |
| 9.36 | Champion | Omega |
| 8.28 | Wizard | Omega |
| 6.84 | King | FIDE |
| 5.76 | Knight | FIDE |
The score is proportional to the total number of squares controlled by a piece calculated for every square it can occupy in the ten-by-ten grid. Aside from giving a general impression of how one would rank a piece against other pieces, there’s not really a lot that one can tell from this scheme. In this scheme, the Seirawan pieces rank high, and the Omega pieces rank low but only due to their finite ranges. Leapers’ attacks have the distinct advantage of being immune to blocking.
That’s all for now, back to work.
 Ed's Big Plans
Ed's Big Plans