Archive for the ‘Brain’ Category
Searching for a Continuous Bit Parity function
Update: The function being sought is better described as “continuous bit-parity” rather than “Fuzzy XOR”, the title of the post has been changed from “Fuzzy Exclusive OR (XOR)” to reflect that.
About two weeks ago, I was working on a project wherein I needed to define a continuous XOR function. The only stipulations are that (1) the function must either be binary and commutative, or it must be variadic; and (2) the function must be continuous.
In my first attempt, I used the classic arrangement of four binary NAND gates to make an XOR where each NAND gate was replaced with the expression { λ: p, q → 1.0 – pq }. The algebraic product T-norm { λ: p, q → pq } is used instead of the standard fuzzy T-norm { λ: p, q → min(p, q) } in order to keep it continuous. Unfortunately, this attempt does not preserve commutativity, so the search continued.
At this point, Dr. Kremer suggested I consider a shifted sine curve. I eventually chose the equation
{ λ: p[1..n] → 0.5 – 0.5cos(π Σi=1npi) }.
This is shown graphically in the below figure …
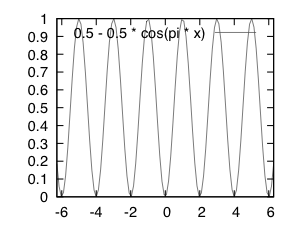
# gnuplot source ... set xrange[-2*pi:2*pi] set output "a.eps" set terminal postscript eps size 2.0, 1.5 plot 0.5 - 0.5 * cos(pi * x)
This can be considered a variadic function because it takes the sum of all fuzzy bits pi in a given string and treats the arguments the same no matter the number of bits n.
Whenever the sum of all bits is equal to an even number, the function returns a zero — whenever the sum is an odd number, the function returns a one. This function offers a continuous (although potentially meaningless) value between integer values of the domain and can handle bitstrings of any length.
If you’re aware of a purely binary Fuzzy XOR (instead of variadic) that is a legal extension of classic XOR, continuous, and commutative — please let me know for future reference 😀
C & Math: Sieve of Eratosthenes with Wheel Factorization
In the first assignment of Computer Security, we were to implement The Sieve of Eratosthenes. The instructor gives a student the failing grade of 6/13 for a naive implementation, and as we increase the efficiency of the sieve, we get more marks. There are the three standard optimizations: (1) for the current prime being considered, start the indexer at the square of the current prime; (2) consider only even numbers; (3) end crossing out numbers at the square root of the last value of the sieve.
Since the assignment has been handed in, I’ve decided to post my solution here as I haven’t seen C code on the web which implements wheel factorization.
We can think of wheel factorization as an extension to skipping all even numbers. Since we know that all even numbers are multiples of two, we can just skip them all and save half the work. By the same token, if we know a pattern of repeating multiples corresponding to the first few primes, then we can skip all of those guaranteed multiples and save some work.
The wheel I implement skips all multiples of 2, 3 and 5. In Melissa O’Neill’s The Genuine Sieve of Erastothenes, an implementation of the sieve with a priority queue optimization is shown in Haskell while wheel factorization with the primes 2, 3, 5 and 7 is discussed. The implementation of that wheel (and other wheels) is left as an exercise for her readers 😛
But first, let’s take a look at the savings of implementing this wheel. Consider the block of numbers in modulo thirty below corresponding to the wheel for primes 2, 3 and 5 …
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
Only the highlighted numbers need to be checked to be crossed out during sieving since the remaining values are guaranteed to be multiples of 2, 3 or 5. This pattern repeats every thirty numbers which is why I say that it is in modulo thirty. We hence skip 22/30 of all cells by using the wheel of thirty — a savings of 73%. If we implemented the wheel O’Neill mentioned, we would skip 77% of cells using a wheel of 210 (for primes 2, 3, 5 and 7).
(Note that the highlighted numbers in the above block also correspond to the multiplicative identity one and numbers which are coprime to 30.)
Below is the final code that I used.
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
const unsigned int SIEVE = 15319000;
const unsigned int PRIME = 990000;
int main(void) {
unsigned char* sieve = calloc(SIEVE + 30, 1); // +30 gives us incr padding
unsigned int thisprime = 7;
unsigned int iprime = 4;
unsigned int sieveroot = (int)sqrt(SIEVE) +1;
// Update: don't need to zero the sieve - using calloc() not malloc()
sieve[7] = 1;
for(; iprime < PRIME; iprime ++) {
// ENHANCEMENT 3: only cross off until square root of |seive|.
if(thisprime < sieveroot) {
// ENHANCEMENT 1: Increment by 30 -- 4/15 the work.
// ENHANCEMENT 2: start crossing off at prime * prime.
int i = (thisprime * thisprime);
switch (i % 30) { // new squared prime -- get equivalence class.
case 1:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 6;
case 7:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 4;
case 11:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 2;
case 13:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 4;
case 17:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 2;
case 19:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 4;
case 23:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 6;
case 29:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 1; // 29 + 1 (mod 30) = 0 -- just in step
}
for(; i < SIEVE; i += 30) {
if(!sieve[i+1] && !((i+1) % thisprime)) sieve[i+1] = 1;
if(!sieve[i+7] && !((i+7) % thisprime)) sieve[i+7] = 1;
if(!sieve[i+11] && !((i+11) % thisprime)) sieve[i+11] = 1;
if(!sieve[i+13] && !((i+13) % thisprime)) sieve[i+13] = 1;
if(!sieve[i+17] && !((i+17) % thisprime)) sieve[i+17] = 1;
if(!sieve[i+19] && !((i+19) % thisprime)) sieve[i+19] = 1;
if(!sieve[i+23] && !((i+23) % thisprime)) sieve[i+23] = 1;
if(!sieve[i+29] && !((i+29) % thisprime)) sieve[i+29] = 1;
}
}
{
int i = thisprime;
switch (i % 30) { // write down the next prime in 'thisprime'.
case 1:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 6;
case 7:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 4;
case 11:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 2;
case 13:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 4;
case 17:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 2;
case 19:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 4;
case 23:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 6;
case 29:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 1;
}
for(; i < SIEVE; i += 30) {
if(!sieve[i+1]) {thisprime = i+1; sieve[i+1] = 1; goto done;}
if(!sieve[i+7]) {thisprime = i+7; sieve[i+7] = 1; goto done;}
if(!sieve[i+11]) {thisprime = i+11; sieve[i+11] = 1; goto done;}
if(!sieve[i+13]) {thisprime = i+13; sieve[i+13] = 1; goto done;}
if(!sieve[i+17]) {thisprime = i+17; sieve[i+17] = 1; goto done;}
if(!sieve[i+19]) {thisprime = i+19; sieve[i+19] = 1; goto done;}
if(!sieve[i+23]) {thisprime = i+23; sieve[i+23] = 1; goto done;}
if(!sieve[i+29]) {thisprime = i+29; sieve[i+29] = 1; goto done;}
}
done:;
}
}
printf("%d\n", thisprime);
free(sieve);
return 0;
}
Notice that there is a switch construct — this is necessary because we aren’t guaranteed that the first value to sieve for a new prime (or squared prime) is going to be an even multiple of thirty. Consider sieving seven — the very first prime to consider. We start by considering 72 = 49. Notice 49 (mod 30) is congruent to 19. The switch statement incrementally moves the cursor from the 19th equivalence class to the 23rd, to the 29th before pushing it one integer more to 30 — 30 (mod 30) is zero — and so we are able to continue incrementing by thirty from then on in the loop.
The code listed is rigged to find the 990 000th prime as per the assignment and uses a sieve of predetermined size. Note that if you want to use my sieve code above to find whichever prime you like, you must also change the size of the sieve. If you take a look at How many primes are there? written by Chris K. Caldwell, you’ll notice a few equations that allow you to highball the nth prime of your choosing, thereby letting you calculate that prime with the overshot sieve size.
Note also that this sieve is not the most efficient. A classmate of mine implemented The Sieve of Atkin which is magnitudes faster than this implementation.
 Ed's Big Plans
Ed's Big Plans