Archive for the ‘Bitstring’ tag
Searching for a Continuous Bit Parity function
Update: The function being sought is better described as “continuous bit-parity” rather than “Fuzzy XOR”, the title of the post has been changed from “Fuzzy Exclusive OR (XOR)” to reflect that.
About two weeks ago, I was working on a project wherein I needed to define a continuous XOR function. The only stipulations are that (1) the function must either be binary and commutative, or it must be variadic; and (2) the function must be continuous.
In my first attempt, I used the classic arrangement of four binary NAND gates to make an XOR where each NAND gate was replaced with the expression { λ: p, q → 1.0 – pq }. The algebraic product T-norm { λ: p, q → pq } is used instead of the standard fuzzy T-norm { λ: p, q → min(p, q) } in order to keep it continuous. Unfortunately, this attempt does not preserve commutativity, so the search continued.
At this point, Dr. Kremer suggested I consider a shifted sine curve. I eventually chose the equation
{ λ: p[1..n] → 0.5 – 0.5cos(π Σi=1npi) }.
This is shown graphically in the below figure …
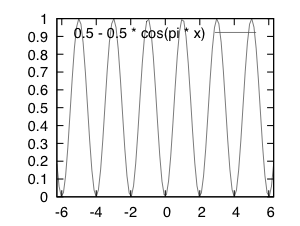
# gnuplot source ... set xrange[-2*pi:2*pi] set output "a.eps" set terminal postscript eps size 2.0, 1.5 plot 0.5 - 0.5 * cos(pi * x)
This can be considered a variadic function because it takes the sum of all fuzzy bits pi in a given string and treats the arguments the same no matter the number of bits n.
Whenever the sum of all bits is equal to an even number, the function returns a zero — whenever the sum is an odd number, the function returns a one. This function offers a continuous (although potentially meaningless) value between integer values of the domain and can handle bitstrings of any length.
If you’re aware of a purely binary Fuzzy XOR (instead of variadic) that is a legal extension of classic XOR, continuous, and commutative — please let me know for future reference 😀
 Ed's Big Plans
Ed's Big Plans