Archive for the ‘C Sharp’ tag
C# & Science: A 2D Heatmap Visualization Function (PNG)
Today, let’s take advantage of the bitmap writing ability of C# and output some heatmaps. Heatmaps are a nice visualization tool as they allow you to summarize numeric continuous values as colour intensities or hue spectra. It’s far easier for the human to grasp a general trend in data via a 2D image than it is to interpret a giant rectangular matrix of numbers. I’ll use two examples to demonstrate my heatmap code. The function provided is generalizable to all 2D arrays of doubles so I welcome you to download it and try it yourself.
>>> Attached: ( tgz | zip — C# source: demo main, example data used below, makefile ) <<<
Let’s start by specifying the two target colour schemes.
- RGB-faux-colour {blue = cold, green = medium, red = hot} for web display
- greyscale {white = cold, black = hot} suitable for print
Next, let’s take a look at the two examples.
Example Heat Maps 1: Bioinformatics Sequence Alignments — Backtrace Matrix
Here’s an application of heat maps to sequence alignments. We’ve visualized the alignment traces in the dynamic programming score matrices of local alignments. Here, a pair of tryptophan-aspartate-40 protein sequences are aligned so that you can quickly pick out two prominent traces with your eyes. The highest scoring spot is in red — the highest scoring trace carries backward and upward on a diagonal from that spot.
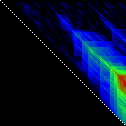

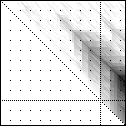
The left heatmap is shown in RGB-faux-colour decorated with a white diagonal. The center heatmap is shown in greyscale with no decorations. The right heatmap is decorated with a major diagonal, borders, lines every 100 values and ticks every ten values. Values correspond to amino acid positions where the top left is (0, 0) of the alignment.
Example Heat Maps 2: Feed Forward Back Propagation Network — Weight Training
Here’s another application of heat maps. This time we’ve visualized the training of neural network weight values. The weights are trained over 200 epochs to their final values. This visualization allows us to see the movement of weights from pseudorandom noise (top) to their final values (bottom).
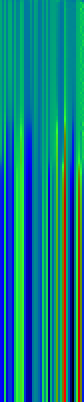

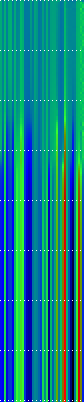
Shown above are the weight and bias values for a 2-input, 4-hidden-node, 4-hidden-node, 2-output back-propagation feed-forward ANN trained on the toy XOR-EQ problem. The maps are rendered as RGB-faux-colour (left); greyscale (center); and RGB-faux-colour decorated with horizontal lines every 25 values (=50px) (right). Without going into detail, the leftmost 12 columns bridge inputs to the first hidden layer, the next 20 columns belong to the next weight layer, and the last 10 columns bridge to the output layer.
Update: I changed the height of the images of this example to half their original height — the horizontal lines now occur every 25 values (=25px).
C# Functions
This code makes use of two C# features — (1) function delegates and (2) optional arguments. If you also crack open the main file attached, you’ll notice I also make use of a third feature — (3) named arguments. A function delegate is used so that we can define and select which heat function to use to transform a three-tuple of double values (real, min, max) into a three-tuple of byte values (R, G, B). Optional arguments are used because the function signature has a total of twelve arguments. Leaving some out with sensible default values makes a lot of sense. Finally, I use named arguments in the main function because they allow me to (1) specify my optional arguments in a logical order and (2) read which arguments have been assigned without looking at the function signature.
Heat Functions
For this code to work, heat functions must match this delegate signature. Arguments: val is the current value, min is the lowest value in the matrix and max is the highest value in the matrix; we use min and max for normalization of val.
public delegate byte[] ValueToPixel(double val, double min, double max);
This is the RGB-faux-colour function that breaks apart the domain of heats and assigns it some amount of blue, green and red.
public static byte[] FauxColourRGB(double val, double min, double max) {
byte r = 0;
byte g = 0;
byte b = 0;
val = (val - min) / (max - min);
if( val <= 0.2) {
b = (byte)((val / 0.2) * 255);
} else if(val > 0.2 && val <= 0.7) {
b = (byte)((1.0 - ((val - 0.2) / 0.5)) * 255);
}
if(val >= 0.2 && val <= 0.6) {
g = (byte)(((val - 0.2) / 0.4) * 255);
} else if(val > 0.6 && val <= 0.9) {
g = (byte)((1.0 - ((val - 0.6) / 0.3)) * 255);
}
if(val >= 0.5 ) {
r = (byte)(((val - 0.5) / 0.5) * 255);
}
return new byte[]{r, g, b};
}
This is a far simpler greyscale function.
public static byte[] Greyscale(double val, double min, double max) {
byte y = 0;
val = (val - min) / (max - min);
y = (byte)((1.0 - val) * 255);
return new byte[]{y, y, y};
}
Heatmap Writer
The function below is split into a few logical parts: (1) we get the minimum and maximum heat values to normalize intensities against; (2) we set the pixels to the colours we want; (3) we add the decorations (borders, ticks etc.); (4) we save the file.
public static void SaveHeatmap(
string fileName, double[,] matrix, ValueToPixel vtp,
int pixw = 1, int pixh = 1,
Color? decorationColour = null,
bool drawBorder = false, bool drawDiag = false,
int hLines = 0, int vLines = 0, int hTicks = 0, int vTicks = 0)
{
var rows = matrix.GetLength(0);
var cols = matrix.GetLength(1);
var bitmap = new Bitmap(rows * pixw, cols * pixh);
//Get min and max values ...
var min = Double.PositiveInfinity;
var max = Double.NegativeInfinity;
for(int i = 0; i < matrix.GetLength(0); i ++) {
for(int j = 0; j < matrix.GetLength(1); j ++) {
max = matrix[i,j] > max? matrix[i,j]: max;
min = matrix[i,j] < min? matrix[i,j]: min;
}
}
//Set pixels ...
for(int j = 0; j < bitmap.Height; j ++) {
for(int i = 0; i < bitmap.Width; i ++) {
var triplet = vtp(matrix[i / pixw, j / pixh], min, max);
var color = Color.FromArgb(triplet[0], triplet[1], triplet[2]);
bitmap.SetPixel(i, j, color);
}
}
//Decorations ...
var dc = decorationColour ?? Color.Black;
for(int i = 0; i < bitmap.Height; i ++) {
for(int j = 0; j < bitmap.Width; j ++) {
if(drawBorder) {
if(i == 0 || i == bitmap.Height -1) {
// Top and Bottom Borders ...
bitmap.SetPixel(j, i, dc);
} else if(j == 0 || j == bitmap.Width -1) {
// Left and Right Borders ...
bitmap.SetPixel(j, i, dc);
}
}
if(bitmap.Width == bitmap.Height && drawDiag && (i % 2 == 0)) {
// Major Diagonal ... (only draw if square image +explicit)
bitmap.SetPixel(i, i, dc);
}
//Zeroed lines and zeroed ticks are turned off.
if(hLines != 0 && i % (hLines*pixh) == 0) {
if(j % (2*pixw) == 0) {
//Horizontal Bars ...
bitmap.SetPixel(j, i, dc);
}
} else if(hTicks != 0 && i % (hTicks*pixh) == 0) {
// Dots: H-Spacing
if(vTicks != 0 && j % (vTicks*pixw) == 0) {
// Dots: V-Spacing
bitmap.SetPixel(j, i, dc);
}
} else if(i % (2*pixh) == 0) {
if(vLines != 0 && j % (vLines*pixw) == 0) {
//Vertical Bars
bitmap.SetPixel(j, i, dc);
}
}
}
}
//Save file...
bitmap.Save(fileName, ImageFormat.Png);
bitmap.Dispose();
}
Happy mapping 😀
Compatibility Notes: The C# code discussed was developed with Mono using Monodevelop. All code is compatible with the C#.NET 4.0 specification and is forward compatible. I’ve linked in two assemblies — (1) -r:System.Core for general C#.Net 3.5~4.0 features, and (2) r:System.Drawing to write out PNG files. If you need an overview of how to set up Monodevelop to use the System.Drawing assembly, see C Sharp PNG Bitmap Writing with System.Drawing in my notebook.
C# & Bioinformatics: Edit Strings and Local Alignment Subprofiles
Alternatively: The awful finite string manipulation bug that took me forever to fix.
Update: Code last update 2010 Dec. 12 (branch logic fixed: gave default “else” case highest priority instead).
Every so often, a bug creeps in during the implementation of a utility function that halts an entire project until it can be fixed. I bumped into one that was so insidious — so retrospectively obvious — that I must share it with you. This particular bug has to do with the way Edit Strings behave when you use them to represent changes done during a Local Alignment rather than a Global Alignment.
Those of you who have looked into MUSCLE may have seen the 2004 BMC paper that goes into great detail about its implementation. In it, Dr. Edgar describes Edit Strings (e-strings) — these are integer strings which keep track of the edits performed on a sequence in order to insert gaps in the correct locations corresponding to an alignment.
I’ve previously discussed and explained e-strings and their use in sequence alignment here and also how to convert alignment strings (a recording of site-to-site insertions/deletions/substitutions) to edit strings here.
E-Strings in Local Alignments
E-strings weren’t originally designed with local alignments in mind — but that’s OK. We can make a few adjustments that will let us keep track of gaps the way we intend them. In a global alignment, all tokens (characters) in each of the aligned sequences are considered. In a local alignment, we need to be able to specify two aligned subsequences rather than the alignment of two full sequences. We can add a simple integer offset to indicate the number of positions since the beginning of aligned sequences to specify the start position of each subsequence.
These are two sequences s and t — (to keep things easy to visualize, I’ve just used characters from the English alphabet).
s = DEIJKLMNOPQRSTUVWXYZ t = ABCDEFGHIJKLMNOUVWXY
Assume that the following is the optimal global alignment of s and t.
s(global) = ---DE---IJKLMNOPQRSTUVWXYZ t(global) = ABCDEFGHIJKLMNO-----UVWXY-
The corresponding edit strings for s and t are es and et respectively.
e(s, global) = < -3, 2, -3, 18 > e(t, global) = < 15, -5, 5, -1 >
Remember, we can take the sum of the absolute values in two edit strings corresponding to the same alignment to be sure that they contain the number of sites. This is true because a site in a given sequence or profile must be either an amino acid (in a sequence) or a distribution of amino acids (in a profile) or a gap (in either). In this case, the absolute values of both es and et correctly add up to 26.
Now let’s adapt the above to local alignments.
The corresponding optimal local alignment for s and t is as follows.
s(local) = DE---IJKLMNOPQRSTUVWXY t(local) = DEFGHIJKLMNO-----UVWXY
The edit strings only need an offset to specify the correct start position in each sequence. Remember that our indexing is zero based, so the position for the character “A” was at position zero.
e(s, local) = 3 + < 2, -3, 17 > e(t, local) = 3 + < 12, -5, 5 >
It’s a pretty straight forward fix. Notice that the absolute values of the integers inside the vectors now only sum up to 22 (corresponding to the sites stretching from “D” to “Y”).
Local Alignment E-String Subprofiles
The bug I faced wasn’t in the above however. It only occurred when I needed to specify subprofiles of local alignments. Imagine having a local alignment of two sequences in memory. Imagine now that there is a specific run of aligned sites therein that you are interested in and want to extract. That specific run should be specifiable by using the original sequences and a corresponding pair of e-strings and pair of offsets. Ideally, the new e-strings and offsets should be derived from the e-strings and offsets we had gathered from performing the original local alignment. We call this specific run of aligned sites a subprofile.
As you will see, this bug is actually a result of forgetting to count the number of gaps needed that occur after the original local alignment offset and before where the new subprofile should start. Don’t worry, this will become clearer with an example.
For the local alignment of s and t, I want to specify a subprofile stretching from the site at letter “I” to the site at letter “V”.
s(local) = DE---IJKLMNOPQRSTUVWXY → s(subprofile) = IJKLMNOPQRSTUV t(local) = DEFGHIJKLMNO-----UVWXY → t(subprofile) = IJKLMNO-----UV
What do you suppose the edit string to derive would be?
Let’s puzzle this out — we want to take a substring from each s and t from position 5 to position 18 of the local alignment as shown below …
Position: 0 0 1 2
0 5 8 1
s(local) = DE---IJKLMNOPQRSTUVWXY →
s(subprofile) = IJKLMNOPQRSTUV
| | | |
t(local) = DEFGHIJKLMNO-----UVWXY →
t(subprofile) = IJKLMNO-----UV
| |
|<- Want ->|
Let’s break this down further and get first the vector part of the e-string and then the offset part of the e-string.
Getting the Vector part of the Edit String
Remember, we’re trying to get an edit string that will operate on the original sequences s, t and return ssubprofile, tsubprofile. Getting the vector part of the estring is straight forward, you literally find all of the sites specified in the subsequence and save them. Since we want positions [5, 18] in the local edit strings, we retrieve the parts of the edit strings which correspond to those sites (we’ll ignore offsets for now). To visualize this site-to-site mapping, let’s decompose our local estrings into something I call unit-estrings — an equivalent estring which only uses positive and negative ones (given as “+” and “-” below in the unit vectors us, ut for s, t respectively).
Position: 0 0 1 2
0 5 8 1
s(local) = D E - - - I J K L M N O P Q R S T U V W X Y
e(s, vector) = < 2, -3, 17 > -> u(s) = < + + - - - + + + + + + + + + + + + + + + + + >
e(s, newvec) = < 14 > <- < + + + + + + + + + + + + + + >
|<- want! ->|
e(t, newvec) = < 7, -5, 2 > <- < + + + + + + + - - - - - + + >
e(t, vector) = < 12, -5, 5 > -> u(t) = < + + + + + + + + + + + + - - - - - + + + + + >
t(local) = D E F G H I J K L M N O - - - - - U V W X Y
We retrieve as our new vectors es, newvec = < 14 > and et, newvec = < 7, -5, 2 >. Notice that the integer vector elements are just a count of the runs of positive and negative ones in the subprofile region that we want.
Getting the Offset part of the Edit String (the Right way)
This part gets a bit tricky. The offset is a sum of three items.
- The offset from the original sequence to the local alignment.
- The offset from the local alignment to the subprofile.
- The negative of all of the gap characters that are inserted in the local alignment until the start of the subprofile.
The below diagram shows where each of these values come from.
s = DEIJKLMNOPQRSTUVWXYZ
s(local) = DE---IJKLMNOPQRSTUVWXY -> +0 -- offset from original to local
s(subprofile) = .....IJKLMNOPQRSTUV -> +5 -- offset from local to subprofile
--- -> -3 -- gaps: local start to subprofile start
=> +2 == TOTAL
| |
t = ABCDEFGHIJKLMNOUVWXY
t(local) = ...DEFGHIJKLMNO-----UVWXY -> +3 -- offset from original to local
t(subprofile) = .....IJKLMNO-----UV -> +5 -- offset from local to subprofile
-> -0 -- gaps: local start to subprofile start
=> +8 == TOTAL
You might be wondering about the weird gap subtraction for sequence s. This is the solution to my bug! We need this gap subtraction! When you forget to subtract these gaps, you end up with an alignment that is incorrect where the subprofile of s starts too late. But why is this so? When we transform a sequence from the original to the subprofile, the gaps that we’ve taken for granted in the local alignment don’t exist yet. This way, we would be mistakenly pushing our subprofile into a position where non-existent gapped sites are virtually aligned to existing amino acid sites in the alignment partner t. This was a very odd concept for me to grasp, so let yourself think on this for a bit if it still doesn’t make sense. … You could always take it for granted too once I show you below that this is indeed the correct solution 😛
The completed edit strings to specify the subprofile from “I” to “V” for the local alignment of s and t are thus:
e(s, subprofile) = 2 + < 14 > e(t, subprofile) = 8 + < 7, -5, 2 >
So let’s make sure these work — let’s apply es, subprofile and et, subprofile onto s and t to see if we get back the correct subprofiles.
>>> apply offsets ... s = DEIJKLMNOPQRSTUVWXYZ : +2 remaining ... s = IJKLMNOPQRSTUVWXYZ t = ABCDEFGHIJKLMNOUVWXY : +8 remaining ... t = IJKLMNOUVWXY >>> apply e-strings ... s = IJKLMNOPQRSTUVWXYZ : < 14 > remaining ... s = IJKLMNOPQRSTUV t = IJKLMNOUVWXY : < 7, -5, 2 > remaining ... t = IJKLMNO : UVWXY : < -5, 2 > remaining ... t = IJKLMNO----- : UVWXY : < 2 > remaining ... t = IJKLMNO-----UV s = IJKLMNOPQRSTUV -- selected subprofile ok. t = IJKLMNO-----UV -- selected subprofile ok.
The above application results in the desired subprofile.
The SubEString Function in C#
The below source code gives the correct implementation in order to find the e-string corresponding to a subprofile with the following arguments. It is an extension function for List<int> — a natural choice since I am treating lists of integer type as edit strings in my project.
- this List<int> u — the local alignment e-string from which to create the subprofile e-string.
- int start — the offset from the left specifying the location of the subprofile with respect to the local alignment.
- int end_before — the indexed site before which we stop; this is different from length since start and end_before are zero-based and are specified from the very start of the local alignment.
- out int lostGaps — returns a negative value to add to the offset — this is the number of gaps that occur between the start of the local alignment and the start of the subprofile.
This function returns a new List<int> e-string as you would expect.
public static List<int> SubEString(
this List<int> u, int start, int end_before, out int lostGaps) {
if(end_before < start) {
Console.Error.WriteLine("Error: end_before < start?! WHY?");
throw new ValueOutOfRange();
}
var retObj = new List<int>();
var consumed = 0; // the amount "consumed" so far.
var remaining_start = start; // subtract "remaining_start" to zero.
var ui = 0; // the current index in the e-string
var uu = 0; // the current element of the e-string
var uu_abs = 0; // the absolute value of the current element
lostGaps = 0; // the number of gaps that is subtracted from the offset.
//START -- dealing with the "start" argument ...
for(; ui < u.Count; ui ++) {
uu = u[ui];
uu_abs = Math.Abs(uu);
if(uu_abs < remaining_start) {
if(uu < 0) lostGaps += uu; //LOSTGAPS
// add uu this time
// it's the fraction of remaining_start we care about.
consumed += uu_abs; // uu smaller than start amount, eat uu.
remaining_start -= uu_abs; // start shrinks by uu.
uu_abs = 0; // no uu left.
uu = 0; // no uu left.
// not done -- go back and get more uu for me to eat.
}
else if(consumed + uu_abs == remaining_start) {
if(uu < 0) lostGaps += -remaining_start; //LOSTGAPS
// -- if thus uu is equal to the start amount,
// count them into LOSTGAPS
// we want to get everything occurring before the subestring start
consumed += remaining_start; // same size -- consume start amount.
uu_abs = 0; // MAD (mutually assured destruction 0 -> 0)
remaining_start = 0; // MAD
uu = 0; // MAD
ui ++; break; // done.
}
else if(consumed + uu_abs > remaining_start) {
if(consumed + uu_abs > end_before && consumed < remaining_start) {
// easier to say ui == u.Count-1?
if(uu < 0) lostGaps += -remaining_start; //LOSTGAPS
uu_abs = (end_before - (consumed + remaining_start));
uu = uu > 0 ? uu_abs : -uu_abs;
retObj.Add(uu);
return retObj;
} else if(consumed + uu_abs < end_before) {
consumed += uu_abs;
// Seemingly wrong -- however:
// push all the way to the end; subtract the beginning of uu_abs
// ensures correct calculation of remaining string
uu_abs -= remaining_start; // remove only start amount.
// we're getting the end half of uu_abs!
if(uu < 0) lostGaps += -remaining_start; //LOSTGAPS
remaining_start = 0; // no start left.
uu = uu > 0 ? uu_abs : -uu_abs; // remaining uu at this ui.
if(uu != 0) retObj.Add(uu); // fixes a zero-entry bug
ui ++; break; // done.
} else {
if(uu < 0) lostGaps += -remaining_start; //LOSTGAPS
uu_abs = (end_before - remaining_start);
uu = uu > 0 ? uu_abs : -uu_abs;
retObj.Add(uu);
return retObj;
}
}
}
//END_BEFORE -- dealing with the "end_before" argument ...
for(; ui < u.Count; ui ++) {
uu = u[ui];
uu_abs = Math.Abs(uu);
if((consumed + uu_abs) == end_before) {
retObj.Add(uu);
break;
} else if((consumed + uu_abs) < end_before) {
retObj.Add(uu);
consumed += uu_abs;
} else /*if((consumed + uu_abs) > end_before)*/ {
uu_abs = end_before - consumed;
uu = uu > 0 ? uu_abs : -uu_abs;
retObj.Add(uu);
break;
}
}
return retObj;
}
I’ve really sent the above code through unit tests and also in practical deployment so it should be relatively bug free. I hope that by posting this here, you can tease out the logic from both the code and the comments and port it to your preferred language. In retrospect, maybe this bug wasn’t so obvious after all. When you think about it, each of the pieces of code and logic are doing exactly what we asked them to. It was only in chaining together an e-string subprofile function along with a local alignment that this thing ever even popped out. Either way, the fix is here. Hopefully it’ll be helpful.
Two Important Notes
- Since global alignments represent the aligned sites of all sequences involved, no offset is used and hence this bug would never occur when specifying a subprofile of a global alignment.
- Gaps that occur in the original sequence don’t affect retrieving the subprofile e-string calculation at all because those gaps DO exist and can be authentically counted into an offset.
Next
I haven’t had a need yet for porting the multiply function (earlier post) from global alignment logic to local alignment logic. If there are any insidious logical flaws like the ones I encountered this time, I’ll be sure to make a post.
C# & Bioinformatics: Indexers & Substitution Matrices
I’ve recently come to appreciate the convenience of C# indexers. What indexers allow you to do is to subscript an object using the familiar bracket notation. I’ve used them for substitution matrices as part of my phylogeny project. Indexers are essentially syntactical sugar that obey the rules of method overloading. I first describe what I think are useful substitution matrix indexers and then a bare bones substitution matrix class (you could use your own). The indexer notation implementation is discussed last, so feel free to skip the preamble if you’re able to deduce what I’m doing.
Note: I’ve only discussed accessors (getters) and not mutators (setters) today.
Some Reasonable Substitution Matrix Indexers
This is the notation you might expect from the indexer notation in C#.
// Let there be a class called SubMatrix which contains data from BLOSUM62.
var sm = new SubMatrix( ... );
// I'll assume you already have some constructors.
int index_of_proline = sm['P'];
// Returns the row or column that corresponds to proline, 14.
char token_at_three = sm[3];
// Returns the amino acid at position three, aspartate.
int score_proline_to_aspartate = sm['P', 'D'];
// Returns the score for a mutation from proline to aspartate, -1.
int score_aspartate_to_proline = sm[3, 14];
// Returns the score for a mutation from aspartate to proline, -1.
An Example Bare Bones Substitution Matrix Class
Let’s say you’ve loaded up the BLOSUM62 and are representing it internally in some 2D array…
// We've keying the rows and columns in the order given by BLOSUM62: // ARNDCQEGHILKMFPSTWYVBZX* (24 rows, columns) int[,] imatrix;
For convenience, let’s say you’ll also keep a dictionary to map at which array position one finds each amino acid…
// Keys = amino acid letters, Values = row or column index Dictionary<char, int> indexOfAA;
Finally, we’ll put these two elements into a class and assume that you’ve already written your own constructors that will take care of the above two items — either from accepting arrays and strings as arguments or by reading from raw files. If this isn’t true and you need more help, feel free to leave a comment and I’ll extend this bare bones example.
// Bare bones class ...
public partial class SubMatrix {
// Properties ...
private int[,] imatrix;
private Dictionary<char, int> indexOfAA;
// Automatic Properties ...
public int Width { // Returns number of rows of the matrix.
get {
return imatrix.GetLength(0);
}
}
// Constructors ...
...
}
I’ve added the automatic property “Width” above — automatic properties are C# members that provide encapsulation: a public face to some arbitrary backend data — you’ve been using these all along when you’ve called “List.Count” or “Array.Length“.
Substitution Matrix Indexer Implementation
You can implement the example substitution matrix indexers as follows. Notice the use of the “this” keyword and square[] brackets[] to specify[] arguments[].
//And finally ...
public partial class SubMatrix {
// Indexers ...
// Give me the row or column index where I can find the token "aa".
public int this[char aa] {
get {
return this.indexOfAA[aa];
}
}
// Give me the amino acid at the row or column index "index".
public char this[int index] {
get {
return this.key[index];
}
}
// Give me the score for mutating token "row" to token "column".
public double this[char row, char column] {
get {
return this.imatrix[this.indexOfAA[row], this.indexOfAA[column]];
}
}
// Give me the score for mutating token at index "row" to index "column".
public double this[int row, int column] {
get {
return this.imatrix[row, column];
}
}
}
Similar constructs are available in Python and Ruby but not Java. I’ll likely cover those later as well as how to set values too.
C# & Bioinformatics: Align Strings to Edit Strings
This post follows roughly from the e-strings (R. Edgar, 2004) topic that I posted about here. The previous source code was listed in Ruby and JS, but this time I’ve used C#.
In this post, I discuss alignment strings (a-strings), then why and how to convert them into edit strings (e-strings). Incidentally, I can’t seem to recover where I first saw alignment strings so tell me if you know.
Alignment strings
When you perform a pairwise sequence alignment, the transformation that you perform on the two sequences is finite. You can record precisely where insertions, deletions and substitutions (or matches) are made. This is useful if you want to retain the original sequences, or later on build a multiple sequence alignment while keeping the history of modifications. There’s a datastructure I’ve seen described called alignment strings, and in it you basically list out the characters ‘I’, ‘D’ and ‘M’ to describe the pairwise alignment.
Consider the example two protein subsequences below.
gi|115372949: GQAGDIRRLQSFNFQTYFVRHYN gi|29827656: SLSTGVSRSFQSVNYPTRYWQ
A global alignment of the two using the BLOSUM62 substitution matrix with the gap penalties -12 to open, -1 to extend yields the following.
gi|115372949: GQAGDIR-----RLQSFNFQTYFVRHYN gi|29827656: SL----STGVSRSFQSVNYPT---RYWQ
The corresponding alignment string looks like this…
gi|115372949: GQAGDIR-----RLQSFNFQTYFVRHYN gi|29827656: SL----STGVSRSFQSVNYPT---RYWQ Align String: MMDDDDMIIIIIMMMMMMMMMDDDMMMM
Remember, the alignment is described such that the top string is modelled as occurring earlier than the bottom string which occurs later — this is why a gap in the top string is an insertion (that new material is inserted in the later, bottom string) while a gap in the bottom string is a deletion (that material is deleted to make the later string). Notice in reality, it doesn’t really matter what’s on top and what’s on bottom– the important thing is that the alignment now contains gaps.
Why we should probably use e-strings instead
An alignment string describes the relationship between two strings and their gaps — we are actually recording some redundant information if we only want to take one string at a time into consideration and the path needed to construct profiles it participates in. The top and bottom sequences are also treated differently, where both ‘M’ and ‘D’ indicates retention of the original characters for the top string and both ‘M’ and ‘I’ indicates retention for the bottom string; the remaining character of course implies the inclusion of a gap character. A pair of e-strings would give each of these sequences their own data structure and allow us to cleanly render the sequences as they appear in the deeper nodes of a phylogenetic tree using the multiply operation described last time.
Here are the corresponding e-strings for the above examples.
gi|115372949: GQAGDIR-----RLQSFNFQTYFVRHYN e-string: < 7, -5, 16 > gi|29827656: SL----STGVSRSFQSVNYPT---RYWQ e-string: < 2, -4, 16, -3, 4 >
Recall that an e-string is a list of alternating positive and negative integers; positive integers mean to retain a substring of the given length from the originating sequence, and negative integers mean to place in a gap of the given length.
Converting a-strings to e-strings
Below is a C# code listing for an implementation I used in my project to convert from a-strings to the more versatile e-strings. The thing is — I really don’t use a-strings to begin with anymore. In earlier versions of my project, I used to keep track of my movement across the score matrix using an a-string by dumping down a ‘D’ for a vertical hop, a ‘I’ for a horizontal hop and a ‘M’ for a diagonal hop. I now just count the number of relevant steps to generate the matching pair of e-strings.
The function below, astring_to_estring takes an a-string (string u) as an argument and returns two e-strings in a list (List<List<int>>) — don’t let that type confuse you, it simply breaks down to a list with two elements in it: the e-string for the top sequence (List<int> v), and the e-string for the bottom sequence (List<int> w).
public static List<List<int>> astring_to_estring(string u) {
/* Defined elsewhere are the constant characters ...
EDITSUB = 'M';
EDITINS = 'I';
EDITDEL = 'D';
*/
var v = new List<int>(); // Top e-string
var w = new List<int>(); // Bottom e-string
foreach(var uu in u) {
if(uu == EDITSUB) { // If we receive a 'M' ...
if(v.Count == 0) { // Working with e-string v (top, keep)
v.Add(1);
} else if(v[v.Count -1] <= 0) {
v.Add(1);
} else {
v[v.Count -1] += 1;
}
if(w.Count == 0) { // Working with e-string w (bottom, gap)
w.Add(1);
} else if(w[w.Count -1] <= 0) {
w.Add(1);
} else {
w[w.Count -1] += 1;
}
} else if(uu == EDITINS) { // If we receive a 'I' ...
if(v.Count == 0) { // Working with e-string v (top, gap)
v.Add(-1);
} else if(v[v.Count -1] >= 0) {
v.Add(-1);
} else {
v[v.Count -1] -= 1;
}
if(w.Count == 0) { // Working with e-string w (bottom, keep)
w.Add(1);
} else if(w[w.Count -1] <= 0) {
w.Add(1);
} else {
w[w.Count -1] += 1;
}
} else if(uu == EDITDEL) { // If we receive a 'D' ...
if(v.Count == 0) { // Working with e-string v (top, keep)
v.Add(1);
} else if(v[v.Count -1] >= 0) {
v[v.Count -1] += 1;
} else {
v.Add(1);
}
if(w.Count == 0) { // Working with e-string w (bottom, keep)
w.Add(-1);
} else if(w[w.Count -1] >= 0) {
w.Add(-1);
} else {
w[w.Count -1] -= 1;
}
}
}
var vw = new List<List<int>>(); // Set up return list ...
vw.Add(v); // Top e-string v added ...
vw.Add(w); // Bottom e-string w added ...
return vw;
}
The conversion back from e-strings to a-strings is also easy, but I don’t cover that today. Enjoy and happy coding 😀
The Null Coalescing Operator (C#, Ruby, JS, Python)
Null coalescence allows you to specify what a statement should evaluate to instead of evaluating to null. It is useful because it allows you to specify that an expression should be substituted with some semantic default instead of defaulting on some semantic null (such as null, None or nil). Here is the syntax and behaviour in four languages I use often — C#, Ruby, JavaScript and Python.
C#
Null coalescencing in C# is very straight forward since it will only ever accept first class objects of the same type (or null) as its operator’s arguments. This restriction is one that exists at compile time; it will refuse to compile if it is asked to compare primitives, or objects of differing types (unless they’re properly cast).
Syntax:
<expression> ?? <expression>
(The usual rules apply regarding nesting expressions, the use of semi-colons in complete statements etc..)
A few examples:
DummyNode a = null; DummyNode b = new DummyNode(); DummyNode c = new DummyNode(); return a ?? b; // returns b return b ?? a; // still returns b DummyNode z = a ?? b; // z gets b return a ?? new DummyNode(); // returns a new dummy node return null ?? a ?? null; // this code has no choice but to return null return a ?? b ?? c; // returns b -- the first item in the chain that wasn't null
No, you’d never really have a bunch of return statements in a row like that — they’re only there to demonstrate what you should expect.
Ruby, Python and Javascript
These languages are less straight forward (i.e. possess picky nuances) since they are happy to evaluate any objects of any class with their coalescing operators (including emulated primitives). These languages however disagree about what the notion of null should be when it comes to numbers, strings, booleans and empty collections; adding to the importance of testing your code!
Syntax for Ruby, Javascript:
<expression> || <expression>
Syntax for Ruby, Python:
<expression> or <expression>
(Ruby is operator greedy :P.)
The use of null coalescence in these languages are the same as they are in C# in that you may nest coalescing expressions as function arguments, use them in return statements, you may chain them together, put in an object constructor as a right-operand expression etc.; the difference is in what Ruby, Python or Javascript will coalesce given a left-expression operand. The below table summarizes what left-expression operand will cause the statement to coalesce into the right-expression operand (i.e. what the language considers to be ‘null’-ish in this use).
| Expression as a left-operand | Does this coalesce in Ruby? | Does this coalesce in Python? | Does this coalesce in JavaScript? |
| nil / None / null | Yes | Yes | Yes |
| [] | No | Yes | No |
| {} | No | Yes | n/a* |
| 0 | No | Yes | Yes |
| 0.0 | No | Yes | Yes |
| “” | No | Yes | Yes |
| ” | No | Yes | Yes |
| false / False / false |
Yes | Yes | Yes |
*Note that in JavaScript, you’d probably want to use an Object instance as an associative array (hash) so that the field names are the keys and the field values are the associated values — doing so means that you can never have a null associative array.
Contrast the above table to what C# will coalesce: strictly “null” objects only.
The null coalescing operator makes me happy. Hopefully it’ll make you happy too.
Brief Hints: C# Nullable Types and Arrays, Special Double Values
Brief Hints: I wanted to show you three things in C# that I’ve been using a lot lately.
Nullable Types are a convenient language construction in C# that allows one to assign a primitive type with null…
double? someval = null; // declares a nullable double called 'someval'.
The question mark suffixing the keyword double makes the variable someval nullable. This was originally designed so that one can retrieve values from LINQ to SQL without checking for nulls (SQL inherently makes this distinction). This could be thought of as yet another construct to make autoboxing primitives more intuitive and more entrenched in the language.
I use nullable types when I need a special ‘unassigned’ value for “find the greatest” or “find the least” kinds of loops.
When we apply Nullable Types to Arrays, we get an array of nullable primitives (arrays are already nullable, being first class objects).
double?[] somevals = new double?[10]; // declares an array called 'somevals' of ten nullable doubles.
An array of primitives is initialized with all values 0.0; whereas an array of primitve?s is initialized with nulls.
Special Double Values are also something that I’ve started using a lot. There are many algorithms I’ve been coming across that use “magic numbers” corresponding to arbitrarily high and arbitrarily low numbers. Instead of using evil magical quantities, I’ve been using Double.PositiveInfinity and Double.NegativeInfinity. C# makes it easy to assign three more special quantities: Double.NaN, Double.MinValue and Double.MaxValue.
Edit: I forgot to mention why I kept italicizing the word primitive. C# doesn’t really have primitives that are exposed to the developer– everything actually IS an object, and the illusion of boxing or not isn’t really relevant. This just makes nullable types all the more logical.
 Ed's Big Plans
Ed's Big Plans