Archive for the ‘Protein Structure’ tag
Idea: Delaunay Simplex Graph Grammar
The Structural Bioinformatics course I’m auditing comes with an independent project for graduate students. I’ve decided to see how feasible and meaningful it is to create a graph rewriting grammar for proteins that have been re-expressed as a Delauney Tessellation.
I was first introduced to the Delauney Tessellation about half a year ago. Such a tessellation is composed of irregular three dimensional tetrahedrons where each vertex corresponds to an amino acid. A hypothetical sphere that is defined by the four points of such a tetrahedron cannot be crossed by a line segment that does not belong to said tetrahedron.
An alphabet in formal languages is a finite set of arbitrarily irreducible tokens that composes the inputs of a language. In this project, I want to see if I can discover a grammar for the language of Delauney protein simplex graphs. Graph rewriting is likened to the collapse of neighbouring tetrahedrons. The tetrahedrons selected are either functionally important, stability important or have a strangely high probability of occurrence. This definition is recursively applied so that previously collapsed points are subject to further collapse in future passes of the algorithm.
When a subgraph is rewritten, two things happen. Some meaning is lost from the original representation of the protein, but that same meaning is captured on a stack of the changes made to the representation. In this way, the protein graph is iteratively simplified, while a stack that records the simplifications indicates all of the salient grammatical productions that have been used.
This stack is what my project is really after. Can a stack based on grammatical production rules for frequency of occurrence render any real information, or is it just noise? I can’t even create a solid angle to drive my hypothesis at this point. … “Yes … ?” …
I’ve seen a lot of weird machine learning algorithms in my line of work… and I attest that it’s hard for a novice to look at a description and decide whether or not it derives anything useful. Keep in mind that the literature is chuck full of things that DO work, and none of the things that didn’t make it. I conjecture that this representation has made me optimistically biased.
This method however IS feasible to deploy on short notice in the scope of an independent project 😀
Squishy TIM Barrel Subunits
Again with the TIM Barrel pictures! Here’s some text about it from my notes…
1a5m (A Urease) is a really interesting protein– it consists of three subunits. Each subunit consists of three unique domains: a very squashed TIM Barrel, an alpha-alpha-alpha-beta-beta domain and a beta-beta-alpha-beta-beta domain. I’m not yet sure what to call little broken alpha helices that have less than two complete turns. The TIM Barrel (though exceedingly asymmetrical) will still be accounted for in the data to be analyzed. The TIM Barrel (566 amino acids) is the alpha subunit of each symmetrical subunit. The remaining two domains are the alpha and beta subunit though PDB is not clear which is which: they each weigh in at 100 and 101 amino acids. 1a5m is part of several solved urease structures in the PDB– the collection: {1A5K, 1A5L, 1A5M, 1A5N, 1A5O} are solved by Pearson et al. (1998).
References
Matthew A. Pearson, Ruth A. Schaller, Linda Overbye Michel, P. Andrew Karplus, and, Robert P. Hausinger (1998). Chemical Rescue of Klebsiella aerogenes Urease Variants Lacking the Carbamylated-Lysine Nickel Ligand. Biochemistry. 37(17):6214-20.
Squishy squishy shapes– the giant pink object in the next picture is actually three such TIM Barrels, each of which belongs to one of the three subunits.
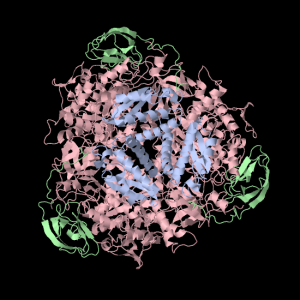
Each of the three subunits are shown separately below…
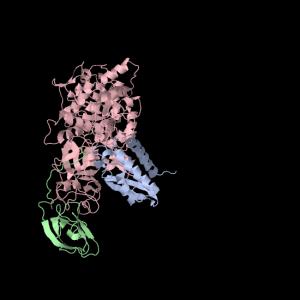 |
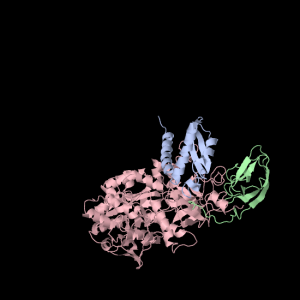 |
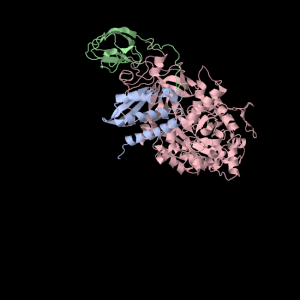 |
Aesthetically pleasing– these images were captured from the JMol output available from RCSB PDB.
 Ed's Big Plans
Ed's Big Plans