Archive for the ‘linkedin’ tag
C & Math: Sieve of Eratosthenes with Wheel Factorization
In the first assignment of Computer Security, we were to implement The Sieve of Eratosthenes. The instructor gives a student the failing grade of 6/13 for a naive implementation, and as we increase the efficiency of the sieve, we get more marks. There are the three standard optimizations: (1) for the current prime being considered, start the indexer at the square of the current prime; (2) consider only even numbers; (3) end crossing out numbers at the square root of the last value of the sieve.
Since the assignment has been handed in, I’ve decided to post my solution here as I haven’t seen C code on the web which implements wheel factorization.
We can think of wheel factorization as an extension to skipping all even numbers. Since we know that all even numbers are multiples of two, we can just skip them all and save half the work. By the same token, if we know a pattern of repeating multiples corresponding to the first few primes, then we can skip all of those guaranteed multiples and save some work.
The wheel I implement skips all multiples of 2, 3 and 5. In Melissa O’Neill’s The Genuine Sieve of Erastothenes, an implementation of the sieve with a priority queue optimization is shown in Haskell while wheel factorization with the primes 2, 3, 5 and 7 is discussed. The implementation of that wheel (and other wheels) is left as an exercise for her readers 😛
But first, let’s take a look at the savings of implementing this wheel. Consider the block of numbers in modulo thirty below corresponding to the wheel for primes 2, 3 and 5 …
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
Only the highlighted numbers need to be checked to be crossed out during sieving since the remaining values are guaranteed to be multiples of 2, 3 or 5. This pattern repeats every thirty numbers which is why I say that it is in modulo thirty. We hence skip 22/30 of all cells by using the wheel of thirty — a savings of 73%. If we implemented the wheel O’Neill mentioned, we would skip 77% of cells using a wheel of 210 (for primes 2, 3, 5 and 7).
(Note that the highlighted numbers in the above block also correspond to the multiplicative identity one and numbers which are coprime to 30.)
Below is the final code that I used.
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
const unsigned int SIEVE = 15319000;
const unsigned int PRIME = 990000;
int main(void) {
unsigned char* sieve = calloc(SIEVE + 30, 1); // +30 gives us incr padding
unsigned int thisprime = 7;
unsigned int iprime = 4;
unsigned int sieveroot = (int)sqrt(SIEVE) +1;
// Update: don't need to zero the sieve - using calloc() not malloc()
sieve[7] = 1;
for(; iprime < PRIME; iprime ++) {
// ENHANCEMENT 3: only cross off until square root of |seive|.
if(thisprime < sieveroot) {
// ENHANCEMENT 1: Increment by 30 -- 4/15 the work.
// ENHANCEMENT 2: start crossing off at prime * prime.
int i = (thisprime * thisprime);
switch (i % 30) { // new squared prime -- get equivalence class.
case 1:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 6;
case 7:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 4;
case 11:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 2;
case 13:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 4;
case 17:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 2;
case 19:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 4;
case 23:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 6;
case 29:
if(!sieve[i] && !(i % thisprime)) {sieve[i] = 1;}
i += 1; // 29 + 1 (mod 30) = 0 -- just in step
}
for(; i < SIEVE; i += 30) {
if(!sieve[i+1] && !((i+1) % thisprime)) sieve[i+1] = 1;
if(!sieve[i+7] && !((i+7) % thisprime)) sieve[i+7] = 1;
if(!sieve[i+11] && !((i+11) % thisprime)) sieve[i+11] = 1;
if(!sieve[i+13] && !((i+13) % thisprime)) sieve[i+13] = 1;
if(!sieve[i+17] && !((i+17) % thisprime)) sieve[i+17] = 1;
if(!sieve[i+19] && !((i+19) % thisprime)) sieve[i+19] = 1;
if(!sieve[i+23] && !((i+23) % thisprime)) sieve[i+23] = 1;
if(!sieve[i+29] && !((i+29) % thisprime)) sieve[i+29] = 1;
}
}
{
int i = thisprime;
switch (i % 30) { // write down the next prime in 'thisprime'.
case 1:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 6;
case 7:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 4;
case 11:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 2;
case 13:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 4;
case 17:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 2;
case 19:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 4;
case 23:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 6;
case 29:
if(!sieve[i]) {thisprime = i; sieve[i] = 1; goto done;}
i += 1;
}
for(; i < SIEVE; i += 30) {
if(!sieve[i+1]) {thisprime = i+1; sieve[i+1] = 1; goto done;}
if(!sieve[i+7]) {thisprime = i+7; sieve[i+7] = 1; goto done;}
if(!sieve[i+11]) {thisprime = i+11; sieve[i+11] = 1; goto done;}
if(!sieve[i+13]) {thisprime = i+13; sieve[i+13] = 1; goto done;}
if(!sieve[i+17]) {thisprime = i+17; sieve[i+17] = 1; goto done;}
if(!sieve[i+19]) {thisprime = i+19; sieve[i+19] = 1; goto done;}
if(!sieve[i+23]) {thisprime = i+23; sieve[i+23] = 1; goto done;}
if(!sieve[i+29]) {thisprime = i+29; sieve[i+29] = 1; goto done;}
}
done:;
}
}
printf("%d\n", thisprime);
free(sieve);
return 0;
}
Notice that there is a switch construct — this is necessary because we aren’t guaranteed that the first value to sieve for a new prime (or squared prime) is going to be an even multiple of thirty. Consider sieving seven — the very first prime to consider. We start by considering 72 = 49. Notice 49 (mod 30) is congruent to 19. The switch statement incrementally moves the cursor from the 19th equivalence class to the 23rd, to the 29th before pushing it one integer more to 30 — 30 (mod 30) is zero — and so we are able to continue incrementing by thirty from then on in the loop.
The code listed is rigged to find the 990 000th prime as per the assignment and uses a sieve of predetermined size. Note that if you want to use my sieve code above to find whichever prime you like, you must also change the size of the sieve. If you take a look at How many primes are there? written by Chris K. Caldwell, you’ll notice a few equations that allow you to highball the nth prime of your choosing, thereby letting you calculate that prime with the overshot sieve size.
Note also that this sieve is not the most efficient. A classmate of mine implemented The Sieve of Atkin which is magnitudes faster than this implementation.
C# & Science: A 2D Heatmap Visualization Function (PNG)
Today, let’s take advantage of the bitmap writing ability of C# and output some heatmaps. Heatmaps are a nice visualization tool as they allow you to summarize numeric continuous values as colour intensities or hue spectra. It’s far easier for the human to grasp a general trend in data via a 2D image than it is to interpret a giant rectangular matrix of numbers. I’ll use two examples to demonstrate my heatmap code. The function provided is generalizable to all 2D arrays of doubles so I welcome you to download it and try it yourself.
>>> Attached: ( tgz | zip — C# source: demo main, example data used below, makefile ) <<<
Let’s start by specifying the two target colour schemes.
- RGB-faux-colour {blue = cold, green = medium, red = hot} for web display
- greyscale {white = cold, black = hot} suitable for print
Next, let’s take a look at the two examples.
Example Heat Maps 1: Bioinformatics Sequence Alignments — Backtrace Matrix
Here’s an application of heat maps to sequence alignments. We’ve visualized the alignment traces in the dynamic programming score matrices of local alignments. Here, a pair of tryptophan-aspartate-40 protein sequences are aligned so that you can quickly pick out two prominent traces with your eyes. The highest scoring spot is in red — the highest scoring trace carries backward and upward on a diagonal from that spot.
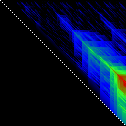

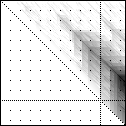
The left heatmap is shown in RGB-faux-colour decorated with a white diagonal. The center heatmap is shown in greyscale with no decorations. The right heatmap is decorated with a major diagonal, borders, lines every 100 values and ticks every ten values. Values correspond to amino acid positions where the top left is (0, 0) of the alignment.
Example Heat Maps 2: Feed Forward Back Propagation Network — Weight Training
Here’s another application of heat maps. This time we’ve visualized the training of neural network weight values. The weights are trained over 200 epochs to their final values. This visualization allows us to see the movement of weights from pseudorandom noise (top) to their final values (bottom).
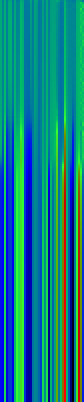

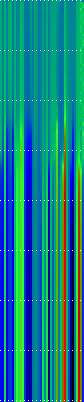
Shown above are the weight and bias values for a 2-input, 4-hidden-node, 4-hidden-node, 2-output back-propagation feed-forward ANN trained on the toy XOR-EQ problem. The maps are rendered as RGB-faux-colour (left); greyscale (center); and RGB-faux-colour decorated with horizontal lines every 25 values (=50px) (right). Without going into detail, the leftmost 12 columns bridge inputs to the first hidden layer, the next 20 columns belong to the next weight layer, and the last 10 columns bridge to the output layer.
Update: I changed the height of the images of this example to half their original height — the horizontal lines now occur every 25 values (=25px).
C# Functions
This code makes use of two C# features — (1) function delegates and (2) optional arguments. If you also crack open the main file attached, you’ll notice I also make use of a third feature — (3) named arguments. A function delegate is used so that we can define and select which heat function to use to transform a three-tuple of double values (real, min, max) into a three-tuple of byte values (R, G, B). Optional arguments are used because the function signature has a total of twelve arguments. Leaving some out with sensible default values makes a lot of sense. Finally, I use named arguments in the main function because they allow me to (1) specify my optional arguments in a logical order and (2) read which arguments have been assigned without looking at the function signature.
Heat Functions
For this code to work, heat functions must match this delegate signature. Arguments: val is the current value, min is the lowest value in the matrix and max is the highest value in the matrix; we use min and max for normalization of val.
public delegate byte[] ValueToPixel(double val, double min, double max);
This is the RGB-faux-colour function that breaks apart the domain of heats and assigns it some amount of blue, green and red.
public static byte[] FauxColourRGB(double val, double min, double max) {
byte r = 0;
byte g = 0;
byte b = 0;
val = (val - min) / (max - min);
if( val <= 0.2) {
b = (byte)((val / 0.2) * 255);
} else if(val > 0.2 && val <= 0.7) {
b = (byte)((1.0 - ((val - 0.2) / 0.5)) * 255);
}
if(val >= 0.2 && val <= 0.6) {
g = (byte)(((val - 0.2) / 0.4) * 255);
} else if(val > 0.6 && val <= 0.9) {
g = (byte)((1.0 - ((val - 0.6) / 0.3)) * 255);
}
if(val >= 0.5 ) {
r = (byte)(((val - 0.5) / 0.5) * 255);
}
return new byte[]{r, g, b};
}
This is a far simpler greyscale function.
public static byte[] Greyscale(double val, double min, double max) {
byte y = 0;
val = (val - min) / (max - min);
y = (byte)((1.0 - val) * 255);
return new byte[]{y, y, y};
}
Heatmap Writer
The function below is split into a few logical parts: (1) we get the minimum and maximum heat values to normalize intensities against; (2) we set the pixels to the colours we want; (3) we add the decorations (borders, ticks etc.); (4) we save the file.
public static void SaveHeatmap(
string fileName, double[,] matrix, ValueToPixel vtp,
int pixw = 1, int pixh = 1,
Color? decorationColour = null,
bool drawBorder = false, bool drawDiag = false,
int hLines = 0, int vLines = 0, int hTicks = 0, int vTicks = 0)
{
var rows = matrix.GetLength(0);
var cols = matrix.GetLength(1);
var bitmap = new Bitmap(rows * pixw, cols * pixh);
//Get min and max values ...
var min = Double.PositiveInfinity;
var max = Double.NegativeInfinity;
for(int i = 0; i < matrix.GetLength(0); i ++) {
for(int j = 0; j < matrix.GetLength(1); j ++) {
max = matrix[i,j] > max? matrix[i,j]: max;
min = matrix[i,j] < min? matrix[i,j]: min;
}
}
//Set pixels ...
for(int j = 0; j < bitmap.Height; j ++) {
for(int i = 0; i < bitmap.Width; i ++) {
var triplet = vtp(matrix[i / pixw, j / pixh], min, max);
var color = Color.FromArgb(triplet[0], triplet[1], triplet[2]);
bitmap.SetPixel(i, j, color);
}
}
//Decorations ...
var dc = decorationColour ?? Color.Black;
for(int i = 0; i < bitmap.Height; i ++) {
for(int j = 0; j < bitmap.Width; j ++) {
if(drawBorder) {
if(i == 0 || i == bitmap.Height -1) {
// Top and Bottom Borders ...
bitmap.SetPixel(j, i, dc);
} else if(j == 0 || j == bitmap.Width -1) {
// Left and Right Borders ...
bitmap.SetPixel(j, i, dc);
}
}
if(bitmap.Width == bitmap.Height && drawDiag && (i % 2 == 0)) {
// Major Diagonal ... (only draw if square image +explicit)
bitmap.SetPixel(i, i, dc);
}
//Zeroed lines and zeroed ticks are turned off.
if(hLines != 0 && i % (hLines*pixh) == 0) {
if(j % (2*pixw) == 0) {
//Horizontal Bars ...
bitmap.SetPixel(j, i, dc);
}
} else if(hTicks != 0 && i % (hTicks*pixh) == 0) {
// Dots: H-Spacing
if(vTicks != 0 && j % (vTicks*pixw) == 0) {
// Dots: V-Spacing
bitmap.SetPixel(j, i, dc);
}
} else if(i % (2*pixh) == 0) {
if(vLines != 0 && j % (vLines*pixw) == 0) {
//Vertical Bars
bitmap.SetPixel(j, i, dc);
}
}
}
}
//Save file...
bitmap.Save(fileName, ImageFormat.Png);
bitmap.Dispose();
}
Happy mapping 😀
Compatibility Notes: The C# code discussed was developed with Mono using Monodevelop. All code is compatible with the C#.NET 4.0 specification and is forward compatible. I’ve linked in two assemblies — (1) -r:System.Core for general C#.Net 3.5~4.0 features, and (2) r:System.Drawing to write out PNG files. If you need an overview of how to set up Monodevelop to use the System.Drawing assembly, see C Sharp PNG Bitmap Writing with System.Drawing in my notebook.
Simple Interactive Phylogenetic Tree Sketches JS+SVG+XHTML
>>> Attached: ( parse_newick_xhtml.js | draw_phylogeny.js — implementation in JS | index.html — demo with IL-1 ) <<<
>>> Attached: ( auto_phylo_diagram.tgz — includes all above, a python script, a demo makefile and IL-1 data ) <<<
In this post, I discuss a Python script I wrote that will convert a Newick Traversal and a FASTA file into a browser-viewable interactive diagram using SVG+JS+XHTML. This method is compatible with WebKit (Safari, Chrome) and Mozilla (Firefox) renderers but not Opera. XHTML doesn’t work with IE, so we’ll have to wait for massive adoption of HTML5 before I can make this work for everyone — don’t worry, it’s coming.
 To the left is what the rendered tree looks like (shown as a screen captured PNG).
To the left is what the rendered tree looks like (shown as a screen captured PNG).
I recommend looking at the demo index.xhtml above if your browser supports it now. The demo will do a far better job than text in explaining exactly what features are possible using this method.
Try clicking on the different nodes and hyperlinks in the demo — notice that the displayed alignment strips away sites (columns) that are 100% gaps so that each node displays only a profile relevant for itself.
I originally intended to explain all the details of the JavaScripts that render and drive the diagram, but I think it’d be more useful to first focus on the Python script and the data input and output from the script.
The Attached Python Script to_xhtml.py found in auto_phylo_diagram.tgz
I’ll explain how to invoke to_xhtml.py with an example below.
python to_xhtml.py IL1fasta.txt IL1tree2.txt "IL-1 group from NCBI CDD (15)" > index.xhtml
Arguments …
- Plain Text FASTA file — IL1fasta.txt
- Plain Text Newick Traversal file — IL1tree2.txt
- Title of the generated XHTML — “IL-1 group from NCBI CDD (15)”
The data I used was generated with MUSCLE with default parameters. I specified the output FASTA with -out and the output second iteration tree with -tree2.
The Attached makefile found in auto_phylo_diagram.tgz
The makefile has two actual rules. If index.html does not exist, it will be regenerated with the above Python script and IL1fasta.txt and IL1tree2.txt. If either IL1fasta.txt or IL1tree2.txt or both do not exist, these files are regenerated using MUSCLE with default parameters on the included example data file ncbi.IL1.cl00094.15.fasta.txt. Running make on the included package shouldn’t do anything since all of the files are included.
The Example Data
The example data comes from the Interleukin-1 group (cd00100) from the NCBI Conserved Domains Database (CDD).
Finally, I’ll discuss briefly the nitty gritty of the JavaScripts found as stand-alones above that are also included in the package.
Part Two of Two
As is the nature of programatically drawing things, this particular task comes with its share of prerequisites.
In a previous — Part 1, I covered Interactive Diagrams Using Inline JS+SVG+XHTML — see that post for compatibility notes and the general method (remember, this technique is a holdover that will eventually be replaced with HTML5 and that the scripts in this post are not compatible with Opera anymore).
In this current post — Part 2, I’ll also assume you’ve seen Parsing a Newick Tree with recursive descent (you don’t need to know it inside and out, since we’ll only use these functions) — if you look at the example index.html attached, you’ll see that we actually parse the Newick Traversal using two functions in parse_newick_xhtml.js — tree_builder() then traverse_tree(). The former converts the traversal to an in-memory binary tree while the latter accepts the root node of said tree and produces an array. This array is read in draw_phylogeny.js by fdraw_tree_svg() which does the actual rendering along with attaching all of the dynamic behaviour.
Parameters ( What are we drawing? )
To keep things simple, let’s focus on three requirements: (1) the tree will me sketched top-down with the root on top and its leaves below; (2) the diagram must make good use of the window width and avoid making horizontal scroll bars (unless it’s absolutely necessary); (3) the drawing function must make the diagram compatible with the overall document object model (DOM) so that we can highlight nodes and know what nodes were clicked to show the appropriate data.
Because of the second condition, all nodes in a given depth of the tree will be drawn at the same time. A horizontal repulsion will be applied so that each level will appear to be centre-justified.
General Strategy
Because we are centre-justifying the tree, we will be drawing each level of the tree simultaneously to calculate the offsets we want for each node. We perform this iteratively for each level of depth of the tree in the function fdraw_tree_svg(). Everything that is written dynamically by JavaScript goes to a div with a unique id. All of the SVG goes to id=”tree_display” and all of the textual output including raster images, text and alignments goes to id=”thoughts”. To attach behaviour to hyperlinks, whether it’s within the SVG or using standard anchor tags, the “onclick” property is defined. In this case, we always call the same function “onclick=javascript:select_node()“. This function accepts a single parameter: the integer serial number that has been clicked.
Additional Behaviour — Images and Links to Databases
After I wrote the first drafts of the JavaScripts, I decided to add two more behaviours in the current version. First, if a particular node name has the letters “GI” in it, the script will attempt to hyperlink it with the proceeding serial number against NCBI. Second, if a particular node name has the letters “PDB” in it, the script will attempt to hyperlink the following identifier against RSCB Protein Database and also pull the first thumbnail with an img tag for the 3D protein structure.
Enjoy!
This was done because I wanted to show a custom alignment algorithm to my advisors. In this demo, I’ve stripped away the custom alignment leaving behind a more general yet pleasing visualizer. I hope that the Python script and JavaScripts are useful to you. Enjoy!
C# & Bioinformatics: Edit Strings and Local Alignment Subprofiles
Alternatively: The awful finite string manipulation bug that took me forever to fix.
Update: Code last update 2010 Dec. 12 (branch logic fixed: gave default “else” case highest priority instead).
Every so often, a bug creeps in during the implementation of a utility function that halts an entire project until it can be fixed. I bumped into one that was so insidious — so retrospectively obvious — that I must share it with you. This particular bug has to do with the way Edit Strings behave when you use them to represent changes done during a Local Alignment rather than a Global Alignment.
Those of you who have looked into MUSCLE may have seen the 2004 BMC paper that goes into great detail about its implementation. In it, Dr. Edgar describes Edit Strings (e-strings) — these are integer strings which keep track of the edits performed on a sequence in order to insert gaps in the correct locations corresponding to an alignment.
I’ve previously discussed and explained e-strings and their use in sequence alignment here and also how to convert alignment strings (a recording of site-to-site insertions/deletions/substitutions) to edit strings here.
E-Strings in Local Alignments
E-strings weren’t originally designed with local alignments in mind — but that’s OK. We can make a few adjustments that will let us keep track of gaps the way we intend them. In a global alignment, all tokens (characters) in each of the aligned sequences are considered. In a local alignment, we need to be able to specify two aligned subsequences rather than the alignment of two full sequences. We can add a simple integer offset to indicate the number of positions since the beginning of aligned sequences to specify the start position of each subsequence.
These are two sequences s and t — (to keep things easy to visualize, I’ve just used characters from the English alphabet).
s = DEIJKLMNOPQRSTUVWXYZ t = ABCDEFGHIJKLMNOUVWXY
Assume that the following is the optimal global alignment of s and t.
s(global) = ---DE---IJKLMNOPQRSTUVWXYZ t(global) = ABCDEFGHIJKLMNO-----UVWXY-
The corresponding edit strings for s and t are es and et respectively.
e(s, global) = < -3, 2, -3, 18 > e(t, global) = < 15, -5, 5, -1 >
Remember, we can take the sum of the absolute values in two edit strings corresponding to the same alignment to be sure that they contain the number of sites. This is true because a site in a given sequence or profile must be either an amino acid (in a sequence) or a distribution of amino acids (in a profile) or a gap (in either). In this case, the absolute values of both es and et correctly add up to 26.
Now let’s adapt the above to local alignments.
The corresponding optimal local alignment for s and t is as follows.
s(local) = DE---IJKLMNOPQRSTUVWXY t(local) = DEFGHIJKLMNO-----UVWXY
The edit strings only need an offset to specify the correct start position in each sequence. Remember that our indexing is zero based, so the position for the character “A” was at position zero.
e(s, local) = 3 + < 2, -3, 17 > e(t, local) = 3 + < 12, -5, 5 >
It’s a pretty straight forward fix. Notice that the absolute values of the integers inside the vectors now only sum up to 22 (corresponding to the sites stretching from “D” to “Y”).
Local Alignment E-String Subprofiles
The bug I faced wasn’t in the above however. It only occurred when I needed to specify subprofiles of local alignments. Imagine having a local alignment of two sequences in memory. Imagine now that there is a specific run of aligned sites therein that you are interested in and want to extract. That specific run should be specifiable by using the original sequences and a corresponding pair of e-strings and pair of offsets. Ideally, the new e-strings and offsets should be derived from the e-strings and offsets we had gathered from performing the original local alignment. We call this specific run of aligned sites a subprofile.
As you will see, this bug is actually a result of forgetting to count the number of gaps needed that occur after the original local alignment offset and before where the new subprofile should start. Don’t worry, this will become clearer with an example.
For the local alignment of s and t, I want to specify a subprofile stretching from the site at letter “I” to the site at letter “V”.
s(local) = DE---IJKLMNOPQRSTUVWXY → s(subprofile) = IJKLMNOPQRSTUV t(local) = DEFGHIJKLMNO-----UVWXY → t(subprofile) = IJKLMNO-----UV
What do you suppose the edit string to derive would be?
Let’s puzzle this out — we want to take a substring from each s and t from position 5 to position 18 of the local alignment as shown below …
Position: 0 0 1 2
0 5 8 1
s(local) = DE---IJKLMNOPQRSTUVWXY →
s(subprofile) = IJKLMNOPQRSTUV
| | | |
t(local) = DEFGHIJKLMNO-----UVWXY →
t(subprofile) = IJKLMNO-----UV
| |
|<- Want ->|
Let’s break this down further and get first the vector part of the e-string and then the offset part of the e-string.
Getting the Vector part of the Edit String
Remember, we’re trying to get an edit string that will operate on the original sequences s, t and return ssubprofile, tsubprofile. Getting the vector part of the estring is straight forward, you literally find all of the sites specified in the subsequence and save them. Since we want positions [5, 18] in the local edit strings, we retrieve the parts of the edit strings which correspond to those sites (we’ll ignore offsets for now). To visualize this site-to-site mapping, let’s decompose our local estrings into something I call unit-estrings — an equivalent estring which only uses positive and negative ones (given as “+” and “-” below in the unit vectors us, ut for s, t respectively).
Position: 0 0 1 2
0 5 8 1
s(local) = D E - - - I J K L M N O P Q R S T U V W X Y
e(s, vector) = < 2, -3, 17 > -> u(s) = < + + - - - + + + + + + + + + + + + + + + + + >
e(s, newvec) = < 14 > <- < + + + + + + + + + + + + + + >
|<- want! ->|
e(t, newvec) = < 7, -5, 2 > <- < + + + + + + + - - - - - + + >
e(t, vector) = < 12, -5, 5 > -> u(t) = < + + + + + + + + + + + + - - - - - + + + + + >
t(local) = D E F G H I J K L M N O - - - - - U V W X Y
We retrieve as our new vectors es, newvec = < 14 > and et, newvec = < 7, -5, 2 >. Notice that the integer vector elements are just a count of the runs of positive and negative ones in the subprofile region that we want.
Getting the Offset part of the Edit String (the Right way)
This part gets a bit tricky. The offset is a sum of three items.
- The offset from the original sequence to the local alignment.
- The offset from the local alignment to the subprofile.
- The negative of all of the gap characters that are inserted in the local alignment until the start of the subprofile.
The below diagram shows where each of these values come from.
s = DEIJKLMNOPQRSTUVWXYZ
s(local) = DE---IJKLMNOPQRSTUVWXY -> +0 -- offset from original to local
s(subprofile) = .....IJKLMNOPQRSTUV -> +5 -- offset from local to subprofile
--- -> -3 -- gaps: local start to subprofile start
=> +2 == TOTAL
| |
t = ABCDEFGHIJKLMNOUVWXY
t(local) = ...DEFGHIJKLMNO-----UVWXY -> +3 -- offset from original to local
t(subprofile) = .....IJKLMNO-----UV -> +5 -- offset from local to subprofile
-> -0 -- gaps: local start to subprofile start
=> +8 == TOTAL
You might be wondering about the weird gap subtraction for sequence s. This is the solution to my bug! We need this gap subtraction! When you forget to subtract these gaps, you end up with an alignment that is incorrect where the subprofile of s starts too late. But why is this so? When we transform a sequence from the original to the subprofile, the gaps that we’ve taken for granted in the local alignment don’t exist yet. This way, we would be mistakenly pushing our subprofile into a position where non-existent gapped sites are virtually aligned to existing amino acid sites in the alignment partner t. This was a very odd concept for me to grasp, so let yourself think on this for a bit if it still doesn’t make sense. … You could always take it for granted too once I show you below that this is indeed the correct solution 😛
The completed edit strings to specify the subprofile from “I” to “V” for the local alignment of s and t are thus:
e(s, subprofile) = 2 + < 14 > e(t, subprofile) = 8 + < 7, -5, 2 >
So let’s make sure these work — let’s apply es, subprofile and et, subprofile onto s and t to see if we get back the correct subprofiles.
>>> apply offsets ... s = DEIJKLMNOPQRSTUVWXYZ : +2 remaining ... s = IJKLMNOPQRSTUVWXYZ t = ABCDEFGHIJKLMNOUVWXY : +8 remaining ... t = IJKLMNOUVWXY >>> apply e-strings ... s = IJKLMNOPQRSTUVWXYZ : < 14 > remaining ... s = IJKLMNOPQRSTUV t = IJKLMNOUVWXY : < 7, -5, 2 > remaining ... t = IJKLMNO : UVWXY : < -5, 2 > remaining ... t = IJKLMNO----- : UVWXY : < 2 > remaining ... t = IJKLMNO-----UV s = IJKLMNOPQRSTUV -- selected subprofile ok. t = IJKLMNO-----UV -- selected subprofile ok.
The above application results in the desired subprofile.
The SubEString Function in C#
The below source code gives the correct implementation in order to find the e-string corresponding to a subprofile with the following arguments. It is an extension function for List<int> — a natural choice since I am treating lists of integer type as edit strings in my project.
- this List<int> u — the local alignment e-string from which to create the subprofile e-string.
- int start — the offset from the left specifying the location of the subprofile with respect to the local alignment.
- int end_before — the indexed site before which we stop; this is different from length since start and end_before are zero-based and are specified from the very start of the local alignment.
- out int lostGaps — returns a negative value to add to the offset — this is the number of gaps that occur between the start of the local alignment and the start of the subprofile.
This function returns a new List<int> e-string as you would expect.
public static List<int> SubEString(
this List<int> u, int start, int end_before, out int lostGaps) {
if(end_before < start) {
Console.Error.WriteLine("Error: end_before < start?! WHY?");
throw new ValueOutOfRange();
}
var retObj = new List<int>();
var consumed = 0; // the amount "consumed" so far.
var remaining_start = start; // subtract "remaining_start" to zero.
var ui = 0; // the current index in the e-string
var uu = 0; // the current element of the e-string
var uu_abs = 0; // the absolute value of the current element
lostGaps = 0; // the number of gaps that is subtracted from the offset.
//START -- dealing with the "start" argument ...
for(; ui < u.Count; ui ++) {
uu = u[ui];
uu_abs = Math.Abs(uu);
if(uu_abs < remaining_start) {
if(uu < 0) lostGaps += uu; //LOSTGAPS
// add uu this time
// it's the fraction of remaining_start we care about.
consumed += uu_abs; // uu smaller than start amount, eat uu.
remaining_start -= uu_abs; // start shrinks by uu.
uu_abs = 0; // no uu left.
uu = 0; // no uu left.
// not done -- go back and get more uu for me to eat.
}
else if(consumed + uu_abs == remaining_start) {
if(uu < 0) lostGaps += -remaining_start; //LOSTGAPS
// -- if thus uu is equal to the start amount,
// count them into LOSTGAPS
// we want to get everything occurring before the subestring start
consumed += remaining_start; // same size -- consume start amount.
uu_abs = 0; // MAD (mutually assured destruction 0 -> 0)
remaining_start = 0; // MAD
uu = 0; // MAD
ui ++; break; // done.
}
else if(consumed + uu_abs > remaining_start) {
if(consumed + uu_abs > end_before && consumed < remaining_start) {
// easier to say ui == u.Count-1?
if(uu < 0) lostGaps += -remaining_start; //LOSTGAPS
uu_abs = (end_before - (consumed + remaining_start));
uu = uu > 0 ? uu_abs : -uu_abs;
retObj.Add(uu);
return retObj;
} else if(consumed + uu_abs < end_before) {
consumed += uu_abs;
// Seemingly wrong -- however:
// push all the way to the end; subtract the beginning of uu_abs
// ensures correct calculation of remaining string
uu_abs -= remaining_start; // remove only start amount.
// we're getting the end half of uu_abs!
if(uu < 0) lostGaps += -remaining_start; //LOSTGAPS
remaining_start = 0; // no start left.
uu = uu > 0 ? uu_abs : -uu_abs; // remaining uu at this ui.
if(uu != 0) retObj.Add(uu); // fixes a zero-entry bug
ui ++; break; // done.
} else {
if(uu < 0) lostGaps += -remaining_start; //LOSTGAPS
uu_abs = (end_before - remaining_start);
uu = uu > 0 ? uu_abs : -uu_abs;
retObj.Add(uu);
return retObj;
}
}
}
//END_BEFORE -- dealing with the "end_before" argument ...
for(; ui < u.Count; ui ++) {
uu = u[ui];
uu_abs = Math.Abs(uu);
if((consumed + uu_abs) == end_before) {
retObj.Add(uu);
break;
} else if((consumed + uu_abs) < end_before) {
retObj.Add(uu);
consumed += uu_abs;
} else /*if((consumed + uu_abs) > end_before)*/ {
uu_abs = end_before - consumed;
uu = uu > 0 ? uu_abs : -uu_abs;
retObj.Add(uu);
break;
}
}
return retObj;
}
I’ve really sent the above code through unit tests and also in practical deployment so it should be relatively bug free. I hope that by posting this here, you can tease out the logic from both the code and the comments and port it to your preferred language. In retrospect, maybe this bug wasn’t so obvious after all. When you think about it, each of the pieces of code and logic are doing exactly what we asked them to. It was only in chaining together an e-string subprofile function along with a local alignment that this thing ever even popped out. Either way, the fix is here. Hopefully it’ll be helpful.
Two Important Notes
- Since global alignments represent the aligned sites of all sequences involved, no offset is used and hence this bug would never occur when specifying a subprofile of a global alignment.
- Gaps that occur in the original sequence don’t affect retrieving the subprofile e-string calculation at all because those gaps DO exist and can be authentically counted into an offset.
Next
I haven’t had a need yet for porting the multiply function (earlier post) from global alignment logic to local alignment logic. If there are any insidious logical flaws like the ones I encountered this time, I’ll be sure to make a post.
Interactive Diagrams Using Inline JS+SVG+XHTML
>>> Attached: ( inline_svg_demo.xhtml — demo using the below technique for a silly drawing ) <<<
Compatibility: The following method doesn’t work for Internet Explorer 8, so if interoperability is really important to you, skip this series! Don’t worry though — Firefox 4.0, Internet Explorer 9 and WebKit (Safari / Chrome) will all natively support HTML5. HTML5 includes inline SVG for HTML so this ad hoc version can be retired when these three products take hold. The below method is compatible with Firefox 3.x, Opera 9.x and the current version of WebKit (Safari 5.x, Chrome 7.x). For display reasons, I’ll show off bitmap files inline while displaying inline SVG in linked pages.
Part One of Two
Part one is for everyone! I describe how to display an SVG inline on a webpage (XHTML) along with some JavaScript driven behaviour (clicking changes a displayed message and CSS defined colours).
Part two is for the bioinformaticians and phylogenists that survive and stick around — I utilize a parsed Newick format traversal to build up the drawing of a tree recursively — then I finish off by reintroducing JavaScript driven interactivity — tree nodes are highlighted via CSS when clicked, and information is displayed for the selected node (perhaps a multiple sequence alignment, a global alignment score, branch lengths — etc.).
( See part two here: Simple Interactive Phylogenetic Tree Sketches JS+SVG+XHTML )
Wait a sec — what do you mean by inline SVG?
Scalable Vector Graphics (SVG) is an XML vector image format. All browsers allow you to specify SVG files to be included into a webpage as an image. What we’ll be discussing here is how to include an SVG image as an XML element directly in a XHTML file — that is, the single webpage file will contain all of the markup for itself and its included SVG images without linking to any external files.
I won’t go into detail about how to make SVG images. You may create them with software like InkScape or by manual manipulation of the raw XML using a text or code editor (which I’ve done in this post). If you do end up using drawing software, simply copy out all of the XML elements with a text editor afterward and inject them into the XHTML page you create.
XHTML File Nuances
Include the following as a attribute of your html tag — this ensures that the browser reading your page knows which document type definition (DTD) to use.
<html xmlns="http://www.w3.org/1999/xhtml"> ... </html>
You must include your SVG with the following tags.
<svg xmlns="http://www.w3.org/2000/svg" width="300" height="300"
xmlns:xlink="http://www.w3.org/1999/xlink">
...
</svg>
In the above, we parameterize the “svg” tag with the correct xml namespace (xmlns) as an attribute. We specify the width and height of the image we want to inline and also specify that we want to be able to use hyperlinks within the SVG image with “xlink”. Notice that both namespace attributes are meant to enable a client browser to correctly render your page.
A Silly Drawing and Target Behaviour
In this post, we’ll be manipulating a picture of a silly face I’ve named Smile Again — if you can render the attached file, the face looks like the one to the right.
The eventual target behaviour we want is as follows. Clicking on different parts of Smile Again’s face causes (1) the displayed message to change and (2) the clicked part to change colours. Notice that I’ll be using JavaScript (JS) to perform both of these functions. We’ll get into the specifics soon — if you’re feeling up to it, you can always go to the attached demo xhtml file now and look at the source to reverse engineer the thing.
We can create this face manually with the following inline SVG code — we’ll start with pure SVG and worry about the JavaScript behaviour afterward.
<svg xmlns="http://www.w3.org/2000/svg" width="300" height="300" xmlns:xlink="http://www.w3.org/1999/xlink"> <circle cx="100" cy="100" r="40" style="fill:white;stroke:black;stroke-width:2" /> <circle cx="100" cy="100" r="20" style="fill:black;stroke:black;stroke-width:2" /> <circle cx="200" cy="100" r="60" style="fill:white;stroke:black;stroke-width:2" /> <circle cx="200" cy="100" r="10" style="fill:black;stroke:black;stroke-width:2" /> <path d="M60 200 C80 300 220 300 240 200 L60 200" style="fill:white;stroke:black;stroke-width:2" /> <path d="M100 235 L200 235" style="fill:white;stroke:black;stroke-width:2" /> <path d="M130 224 L130 246" style="fill:white;stroke:black;stroke-width:2" /> <path d="M150 220 L150 250" style="fill:white;stroke:black;stroke-width:2" /> <path d="M170 224 L170 246" style="fill:white;stroke:black;stroke-width:2" /> </svg>
Each of the XML elements above correspond to a different piece of the SVG image. The first four circles draw the eyes, next the complicated path draws the mouth and the four simpler paths draw the stitches of the teeth.
Changing the Displayed Message with JavaScript
Now that we’ve drawn Smile Again, we want to have it react to mouse clicks. I want to have both the clicked features highlight as well as the displayed message to change. This would be an important feature of actual practical diagrams. To make this task a bit easier to explain, I will break down the behaviour into smaller components and functions and build them back up as I go along. This will also make it a lot easier to read.
Let us focus on just the two circles that makes up Smile Again’s right eye (on the left side of the diagram).
We want our clicks to call a function — in order for that to happen, we need to use anchor tags (hyperlinks) within the SVG. This is made possible with our careful xmlns (namespace) attributes we declared earlier!
<svg xmlns="http://www.w3.org/2000/svg" width="300" height="300"
xmlns:xlink="http://www.w3.org/1999/xlink">
<a xlink:href="#" onclick="javascript:change_thoughts('Oww! My right cornea!')">
<circle cx="100" cy="100" r="40"
style="fill:white;stroke:black;stroke-width:2" />
</a>
<a xlink:href="#" onclick="javascript:change_thoughts('Ouch! My right iris!')">
<circle cx="100" cy="100" r="20"
style="fill:black;stroke:black;stroke-width:2" />
</a>
...
</svg>
Notice that we’ve now enclosed entire clickable elements in anchor tags and have used the “xlink:href” hyperlink attribute. In reality, we can have these links point to actual other webpages. Instead, these point to the same page and call the JavaScript function to change the text in the description called “change_thoughts”. In this case, the output is an expression of pain after being poked in the eye (“Oww! My right cornea!”). We can now define the “change_thoughts” function and also the place where we want our messages to appear.
<head>
...
function change_thoughts(say_this) {
document.getElementById("thoughts").innerHTML = "\"" + say_this + "\""
}
...
</head>
<body>
...
<h2 id = "thoughts" style="font-family:monospace;">
</h2>
...
</body>
The “change_thoughts” function can go in the head or somewhere early in the body of the XHTML. It doesn’t really matter as long as it occurs before the SVG. This function gets an element with the id “thoughts” and changes the HTML inside of it. In the above, I add a pair of double quotes to the string to show. The element with the id “thoughts” is a h2 element — this really could been any valid HTML element. You do however have to place the “thoughts” element somewhere after you declare the “change_thoughts” function.
Changing the Highlighting with JavaScript and CSS
The last thing we want to do is to change the highlighting by making our JavaScript function touch the style (CSS) of the inline SVG element that was clicked. We could use a separate CSS file, but in the spirit of making everything one inlined file, the CSS is specified with the “style” html attribute.
Again, we’ll be looking only at the two circles corresponding to Smile Again’s right eye (I’ve changed the way the lines are broken in the code listing below so that it will actually fit on this page).
<a xlink:href="#"
onclick=
"javascript:change_thoughts('Oww! My right cornea!','right_cornea', '#F00')">
<circle cx="100" cy="100" r="40"
style="fill:white;stroke:black;stroke-width:2"
id="right_cornea" />
</a>
<a xlink:href="#"
onclick=
"javascript:change_thoughts('Ouch! My right iris!', 'right_iris', '#00F')">
<circle cx="100" cy="100" r="20"
style="fill:black;stroke:black;stroke-width:2"
id="right_iris" />
</a>
Here are our two changes. First — each of the SVG elements now have a unique id (“right_cornea”, “right_iris”) so that we can use JS to manipulate each shape independently. Second — we’re now calling a new version of “change_thoughts” — this time, we’re giving the function the id of the shape to highlight and the colour (in hexadecimal) to highlight it with.
Finally, I can show you the new version of “change_thoughts” which will accept the new arguments and change the colours of the shapes.
function change_thoughts(say_this, highlight_this, colour) {
// Say this ...
document.getElementById("thoughts").innerHTML = "\"" + say_this + "\""
// Highlight this ...
var change = document.getElementById(highlight_this)
change.setAttribute("style",
"fill:" + colour + ";stroke:black;stroke-width:5")
}
In the above, we’ve added the code after “// Highlight this …”. We select the element “highlight_this” — remember, the id and colour are given by the function called with mouse clicks in the SVG. We then change the style by overwriting the inline CSS with the new specified fill colour (and a fat black stroke).
We now have a problem — each new mouseclick on a different shape will cause that new shape to highlight. The previous highlighted shape doesn’t automatically revert, and eventually all of the shapes are highlighted. What we need to do now is to improve the “change_thoughts” function one last time with some way to “undo” the previous change, so that new calls to this function will not only highlight the new shape, but will also remove the highlight from the previous shape.
Finishing with an Undo Object to remove previous changes
In the following version, we add an object to behave like a hash in the JavaScript. This hash will take html id attributes as keys, and the previous style as values. This behaves like an “undo” stack since we apply the styles to the elements with the corresponding id before we commit the changes to the new shape.
var _undo_render_hash = new Object
function change_thoughts(say_this, highlight_this, colour) {
// Say this ...
document.getElementById("thoughts").innerHTML = "\"" + say_this + "\""
// Undo previous highlight ...
for(var i in _undo_render_hash) {
document.getElementById(i).setAttribute("style", _undo_render_hash[i])
}
// Reset undo stack ...
_undo_render_hash = new Object
// Highlight this ...
var change = document.getElementById(highlight_this)
_undo_render_hash[highlight_this] = change.getAttribute("style")
change.setAttribute("style",
"fill:" + colour + ";stroke:black;stroke-width:5")
}
Walking through the code, we start with a blank object as the undo stack — this is OK. On the first call of this function, since the undo object is empty, simply nothing is done before the new shape is highlighted. After the first call, all of the changes that were committed in the last call of the function are undone as their original styles are reapplied. We just add the next object to change to the undo object before applying changes to it.
The undo object is treated like a hash here, and in fact, we iterate all of its elements even though we only expect to have captured one id in the last call of the function. This means we can use this undo technique for functions that will modify many shapes with many changes since each of those modifications is iteratively undone in the next call. We must of course ensure that we save the original style of each of these shapes.
Next
At some point, I’ll want to revisit this and combine some of the other JavaScript stuff I’ve shown in this blog before. Displaying a rendered clickable phylogenetic tree is a task I figured out since I needed to quickly visualize some data for my team in my thesis work. Since I’ve already covered parsing a newick tree in this blog, it makes sense to complete the discussion with how I ended up with my phylogeny visualizer.
BioCompiler might start life as BioCOBOL
Update: Matthew has found an even more thorough review paper that discusses computer assisted synthetic biology approaches — it can be found at doi:10.1016/j.copbio.2009.08.007.
The iGEM competition year is running to a close. The teams are headed into November 2010 and have roughly one month left before attending the conference. I’m personally not attending the conference this year — I think the undergraduates will get more out of the experience.
The current year sees our continued efforts to precipitate a dedicated software team — a functioning autonomous unit that will serve to supplement and enhance Waterloo’s impact in the iGEM competition. More importantly, we’re going to do some very interesting science. We’ve had some success talking with other student groups across campus — notably, we should probably talk with the student IEEE/CUBE chapter when we have more work completed. We had involved BIC as well, however, it was early on and we had even less ground to stand upon ( — the primordial software team was mostly interested in BioMortar and BrickLayer at the time — the later project having been taken up by the iGEM Coop students as in Python this year).
This whole BioCompiler business started when Matthew uncovered a nice candidate problem: the compilation of a schematic for behaviour to a fully functioning synthetic biological circuit. Let’s be as precise as we can be here. I mean to say, we will take a description (which could resemble a piece of formal language source code) — and have it compiled into the sequence of BioBricks that will produce the desired behaviour.
This idea has been approached by several groups before — but each time, a different subproblem was considered (this is a reorganization of Matthew’s very nice list here).
- Synthetic biology programming language: Genetic Engineering of Living Cells (GEC) (Microsoft Research) is a project that hones in on a formal language specification.
- Synthetic biology computer assisted design (CAD): Berkeley Software (iGEM 2009) created a suite of items — Eugene (formal language for synthetic biology), Spectacles (visualizer integrating parts with their behaviours), Kepler (a dataflow broker). As well, Berkeley is responsible for the award winning Clotho (iGEM 2008 – Best Software Tool) which is a workbench that connects with the parts registry database (amongst other possible resources).
- Systems biology pathway reaction simulation: Systems Biology Markup Language (SBML), Systems Biology Workbench (SBW) and Jarnac are a set of tools that perform systems biology analysis (which we consider to be an output of synthetic biology). SBML is the formal language, Jarnac is a reaction network simulator (which utilizes JDesigner as a front end) and SBML is a dataflow broker between SBML and Jarnac.
- BioBrick specific pathway simulation: Minnesota’s Team Comparator (iGEM 2008) created SynBioSS — a tool which estimates the concentration of reactants and products given the appropriate BioBricks on a simulated circuit.
Update — here are a few more items thanks to Matthew Gingerich, George Zarubin and Andre Masella.
- Molecular biology and bioinformatics analysis: The European Molecular Biology Open Software Suite (EMBOSS) is a toolkit developed by the European Molecular Biology Network (EMBnet) for bioinformatics. This might not be immediately relevant, but it is interesting. EMBOSS is actually relatively complete. More distantly along this vein, there’s also Bioconductor which focuses mostly on microarray analysis and is implemented in R.
- More synthetic biology computer aided design (CAD): TinkerCell is a GUI-driven piece of software that supports extension with C++ and Python. TinkerCell along with the suite created by Berkeley Software are the two most promising target systems in which to integrate BioCompiler. Finally, there’s GenoCAD which appears to be in an early phase of development — this software looks to emphasize construction with correct syntax and attribute grammars — I’ll have to read more about this.
- Formal laboratory protocol description: BioCoder is another Microsoft research project — the designed language aims to be both human readable and complete for automation. It reminds me of standard operating procedures (SOP) with greater precision. While BioCoder compiles from protocol to automation, we’ll be compiling to circuitry and protocol. BioCoder will give us some insights about the kinds of protocols that others are thinking of.
There is of course more software, but these are the items that we have become most familiar with — that we like — and that we consider to be standards toward which our own work should strive.
Two interesting problems arise when we think about these subproblems. First, the programming languages specified (including Eugene from Berkeley’s CAD suite) are exactly what they claim to be. Formal specifications. This is possible because of how concrete they are. They literally document what a synthetic biology circuit is. But this isn’t too different from what humans have been doing in iGEM all along. Second, the synthetic biology items don’t really seem to talk to the systems biology items — whereas we expect that the two — being input and output — to be inextricably linked. I explain my thoughts on the two below.
Why a programming language?
Andre enlightened me to this the other day. Humans invented programming languages to do two things. On an arrow running from the concrete toward the esoteric, we have the practical concern of compressing the amount of code that we want to write while retaining our programs’ expressiveness. This is the origin of macro systems such as COBOL. On an arrow pointing in the reverse — from the cerebral abstract down to the literal — we have the theoretical concern of mathematical beauty, of completeness. This is the origin of such functional languages like Lisp. For humans to have any hope of creating such a Lisp-like language for synthetic biology — we would need to understand all of the reactionary nuances about it, the system with which we tamper — at least inasmuch as a painful heuristic approximation. This is a feat we are no where near completing though footholds are managed with systems biology.
So here we are, BioCOBOL is the first step. A developing simple — though complete macro-like system that is in league in terms of abstraction with the programming language / CAD -like projects we’ve seen thus far. Only, we aim to increase the efficiency of circuit design; so that the programming language is not a literal mapping of the human document — rather, it is an explanation of behaviour. We will abstract it ever so slightly with each iteration of development — departing further and further away from CAD. A subteam headed by Brandon is currently developing the syntax and search algorithms required for the job — Brandon suggests that a weighted traversal of valid circuits should form our algorithmic primitive. My subteam is attempting to characterize as many known circuits in iGEM as possible — analyzing what pieces of input (stimuli: chemical concentrations, gradients, quora, oscillators) may be compressed for their common usage — what function prototypes already exist ( — reacts to an input: promoters) for compression — what the standard outputs are (analogy to printing error messages: GFP-family) etc. — again in the effort to realize what is losslessly compressible. Our software should eventually provide the correct laboratory protocol as well.
In this sense, we are respecting what a compiler is before we even approach more sophisticated compilation: it transforms a document in one language to another.
Incidentally, I should mention that Jordan and George are working on a modelling problem with the lab team — I’m not clear on the specifics, but I take it they want to pull out some differential equations on a set of promoters.
Why do we care that Synthetic Biology logic should talk to Systems Biology logic?
Finally, it is clear that we will eventually want to become even more abstract — even more mathematically complete, even more expressive. While we may never know enough about systems biology to create BioLISP (in our lifetime), we expect there to be sufficient research for us to discover — and perhaps research we can conduct ourselves to come ever closer. Systems biology allows us to think about synthetic biology in terms of reaction concentrations; free energy etc.. It gives the notion of compilation its own ground; the ground we want to cover. Imagine the perfect BioCompiler — stating the a problem to be compiled in terms of the input and output of the system. Let’s be precise here: I mean to say, the products and reactants or behaviour of our circuit. Let us describe what our circuit will do instead of what our circuit is made of. This — the missing link, this compiler — is the logical final step of BioCompiler.
 Ed's Big Plans
Ed's Big Plans
